题目内容
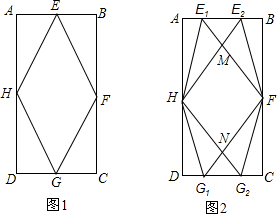
7.如图1,在矩形ABCD中,AB=4cm,BC=8cm.E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE.(1)求证:四边形EFGH是菱形;
(2)如图2,若E1,E2分别从E出发以1cm/s的速度沿射线EA,EB方向运动,同时G1,G2从G出发以同样的速度分别沿射线GD,GC方向运动,E1F与E2H交于点M,G1F与G2H交于点N.设运动的时间为t(s),求四边形E1FG2H与四边形E2HG1F覆盖平面的总面积y与运动时间t之间的函数关系式;
(3)当t为何值时,四边形HMFN为正方形.
分析 (1)连结AC,BD,根据三角形的中位线定理和矩形的对角线相等证明EF=FG=GH=HE,得到答案;
(2)证明△MOH∽△HAE2,求出MO的长,表示出四边形E1FG2H与四边形E2HG1F覆盖平面的总面积y与运动时间t之间的函数关系式;
(3)根据四边形HMFN为正方形时,MO=$\frac{1}{2}$HF,求出时间t.
解答 证明:(1)连结AC,BD,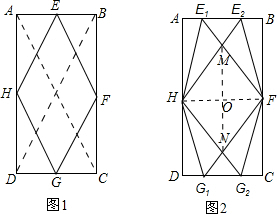
∵E为AB的中点,F为BC的中点,
∴EF为△ABC的中位线∴EF=$\frac{1}{2}$AC
同理HG=$\frac{1}{2}$AC,EH=FG=$\frac{1}{2}$BD
∵矩形ABCD
∴AC=BD
∴EF=FG=GH=HE
∴四边形EFGH是菱形.
(2)连结HF,MN交于点O.
由△MOH∽△HAE2,
∴$\frac{MO}{OH}$=$\frac{AH}{{E}_{2}A}$,
∴,$\frac{MO}{2}$=$\frac{4}{t+2}$,
∴MO=$\frac{8}{t+2}$,
y=2(S△${\;}_{△HF{E}_{1}}$+S${\;}_{△HF{E}_{2}}$-S△HFM)
y=32-$\frac{32}{t+2}$.
(3)∵四边形HMFN是正方形,
∴MO=$\frac{1}{2}$HF
∴$\frac{8}{t+2}$=2
∴t=2.
点评 本题是四边形的综合应用题,掌握三角形中位线定理、菱形的判定定理和正方形的性质是解题的关键,根据题意正确找出辅助线是解决问题的重点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.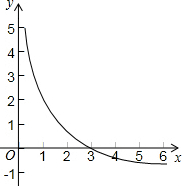 小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )
小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )
 小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )
小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=4 |
15.下列运算正确的是( )
| A. | (a3-a)÷a=a2 | B. | (a3)2=a5 | C. | a3+a2=a5 | D. | a3÷a3=1 |
19.近似数4.73和( )最接近.
| A. | 4.69 | B. | 4.699 | C. | 4.728 | D. | 4.731 |
16.某班“环保小组”的5位同学在一次活动中,捡废弃塑料袋的个数分别为:4,6,10,16,16.这组数据的中位数、众数分别为( )
| A. | 16,16 | B. | 10,10 | C. | 10,16 | D. | 8,16 |