题目内容
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是BC 边上一 动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形,BD的长为______.
边上一 动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形,BD的长为______.
1或2 解析:分三种情况:(1)当∠AFE=90°时,
∵∠EFD=∠B=30°,∴∠AFC=60°,
∵∠ACF=90°,∴∠FAC=30°.
∵BC=3,∴AC= ∴FC=1,BF=BC-FC=2.
∴FC=1,BF=BC-FC=2.
∵BD=DF,∴BD= BF=1.
BF=1.
(2)当∠AEF=90°时,∴∠BED=∠FED= ×90°=45°.
×90°=45°.
∵∠B=30°,∴∠EDB=105°,这与DE⊥BC矛盾,这种情况不可能出现.

(3)当∠EAF=90°时,点F在BC的延长线上,如图,
∵∠EAF=90°,∠BAC=60°,
∴∠CAF=30°.
∵AC= ,∴CF=1,∴BF=BC+CF=4.∵BD=DF,∴BD=
,∴CF=1,∴BF=BC+CF=4.∵BD=DF,∴BD= BF=2.
BF=2.
综上可知,当△AEF为直角三角形时,BD的长为1或2.


练习册系列答案
相关题目




 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( ) D.x≥1
D.x≥1 有意义的最小整数m是________.
有意义的最小整数m是________. .由图可知,相邻两个月中,用电量变化最大的是( )
.由图可知,相邻两个月中,用电量变化最大的是( )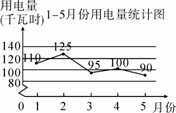
 056年,是永州人民为纪念唐宋八大家之一的柳宗元而筑建.现有三位游客分别参观这三个景点,为了使这三位游客参观完景点后步行返回旅游车上所走的路程总和最短.那么,旅游车等候这三位游客的最佳地点应在( )
056年,是永州人民为纪念唐宋八大家之一的柳宗元而筑建.现有三位游客分别参观这三个景点,为了使这三位游客参观完景点后步行返回旅游车上所走的路程总和最短.那么,旅游车等候这三位游客的最佳地点应在( )