题目内容
5. 如图,AB是⊙O的直径,且AB垂直弦CD于点E,点G是AB上一点,点P为AB延长线上一点,AB=8,CD=4$\sqrt{2}$.
如图,AB是⊙O的直径,且AB垂直弦CD于点E,点G是AB上一点,点P为AB延长线上一点,AB=8,CD=4$\sqrt{2}$.(1)连接GC,GD,试问当GE为何值时,△GDC是等边三角形?
(2)填空:
①当GE=4-2$\sqrt{2}$,四边形GCBD是菱形;
②当PB=4$\sqrt{2}$-4,四边形PCOD是正方形.
分析 (1)把△GDC作为等边三角形,根据等边三角形的性质和三角函数的定义得出GE长度即可;
(2)①根据四边形GCBD是菱形,得出GB和CD互相平分,设BE=x,则GE=x,OE=4-x,由勾股定理得出x即可,
②根据四边形PCOD是正方形,得出OC=PC,由勾股定理得出OP,从而得出PB即可.
解答 解:(1)当GE=2$\sqrt{6}$时,△GDC是等边三角形;
理由如下:∵AB是⊙O的直径,且AB垂直弦CD于点E,
∴GC=GD,CE=DE=$\frac{1}{2}$CD=2$\sqrt{2}$,
∵GE=2$\sqrt{6}$,
∴tanC=$\frac{GE}{CE}$=$\frac{2\sqrt{6}}{2\sqrt{2}}$=$\sqrt{3}$,
∴∠C=60°,
∴△GDC是等边三角形;
(2)①连接OC,如图1,
∵四边形GCBD是菱形,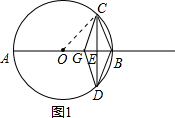
∴BE=GE,
设BE=x,则GE=x,OE=4-x,
∵OC=4,CD=4$\sqrt{2}$,
∴CE=2$\sqrt{2}$,
∴(4-x)2+(2$\sqrt{2}$)2=16,
∴x=4±2$\sqrt{2}$,
∵BE<4,
∴x=4-2$\sqrt{2}$,
∴GE=4-2$\sqrt{2}$;
②如图2,∵四边形PCOD是正方形,
∴OC=PC,
∵OC=4,CD=4$\sqrt{2}$,
∴OP=4$\sqrt{2}$,
∵BO=4,
∴PB=4$\sqrt{2}$-4,
故答案为4-2$\sqrt{2}$,4$\sqrt{2}$-4.
点评 本题考查了菱形的判定,等边三角形的判定定理以及正方形的判定和性质,是一道综合型的题目,难度不大,是中考的常见题型.

练习册系列答案
相关题目
15.与$\sqrt{3}$+1最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.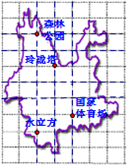 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
10.我国央行公布的数据显示,中国2015年11月外汇储备为34383亿美元.34383亿用科学记数法可表示为( )
| A. | 34.383×1011 | B. | 3.4383×1012 | C. | 3.4383×1013 | D. | 3.4383×1011 |
17.下列图形中,轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.在下列二次根式中,与$\sqrt{a}$是同类二次根式的是( )
| A. | $\sqrt{2a}$ | B. | $\sqrt{3{a}^{2}}$ | C. | 2$\sqrt{a}$ | D. | $\sqrt{{a}^{4}}$ |
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上) 如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).
如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).