题目内容
如图△DAC和△ECB均为等边三角形，AE，BD分别与CD，CE交于点M，N，有如下结论，其中正确的个数是（ ）①△ACE≌△DCB；②CM=CN；③AM=DN．
分析：根据等边三角形性质求出AC=CD，BC=CE，∠ACD=∠BCE=60°，求出∠ACE=∠BCD，根据SAS证△ACE≌△DCB即可；由全等推出∠CAM=∠CDN，根据ASA证△ACM≌△DCN即可．
解答：解：∵△DAC和△ECB均为等边三角形，
∴AC=CD，BC=CE，∠ACD=∠BCE=60°，
∴∠DCE=180°-60°-60°=60°=∠ACD，
∠ACD+∠DCE=∠BCE+∠DCE，
即∠ACE=∠BCD，
∵在△ACE和△DCB中
，
∴△ACE≌△DCB，
∴∠CAM=∠CDN，
∵在△ACM和△DCN中
，
∴△ACM≌△DCN，
∴CM=CN，AM=DN，
∴①②③都正确；
故选A．
∴AC=CD，BC=CE，∠ACD=∠BCE=60°，
∴∠DCE=180°-60°-60°=60°=∠ACD，
∠ACD+∠DCE=∠BCE+∠DCE，
即∠ACE=∠BCD，
∵在△ACE和△DCB中
|
∴△ACE≌△DCB，
∴∠CAM=∠CDN，
∵在△ACM和△DCN中
|
∴△ACM≌△DCN，
∴CM=CN，AM=DN，
∴①②③都正确；
故选A．
点评：本题考查了全等三角形的性质和判定，等边三角形的性质的应用，主要考查了学生的推理能力，题目具有一定的代表性，是一道比较好的题目．
练习册系列答案
相关题目
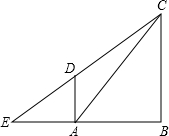相切，D为切点，AD∥BC．
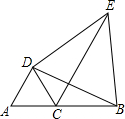（2013•西城区一模）如图，点C在线段AB上，△DAC和△DBE都是等边三角形．
（2013•团风县模拟）如图，点C在线段AB上，△DAC和△DBE都是等边三角形，求证：DA∥EC．
31、如图，△ACD和△ABE都是直角等腰三角形，∠DAC和∠EAB是直角，连接CE．