题目内容
已知:如下图,△ABC中,CD⊥AB于D,AC=4,BC=3,DB=![]() .
.

(1)求DC的长;
(2)求AD的长;
(3)求AB的长;
(4)求证:△ABC是直角三角形.
(1)解:在Rt△DCB中,DC2+DB2=BC2
∴DC2=9-![]()
∴DC=![]()
(2)解:在Rt△ACD中,AD2+CD2=AC2
∴AD2=16-![]()
∴AD=![]()
(3)解:AB=AD+DB=![]() +
+![]() =5
=5
(4)证明:∵AC2+BC2=16+9=25,AB2=25
∴AC2+BC2=AB2
∴∠ACB=90°,
∴△ABC是直角三角形.

练习册系列答案
相关题目
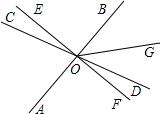 已知:如下图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
已知:如下图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.


