题目内容
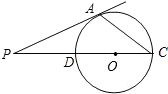如图：P是⊙O的直径CD的延长线上一点，PA是⊙O的切线，A为切点，∠P=40°，则∠ACP=________．
25°
分析：连接OA，由PA是⊙O的切线，则∠OAP=90°，又∠P=40°，则∠AOP=50°，再由圆周角定理得出∠ACP的度数．
解答：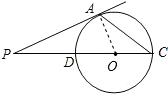
解：连接OA．
由于PA是⊙O的切线，则△APO是直角三角形；
在Rt△APO中，∠P=40°，∠AOP=50°；
再由圆周角定理，∠ACP=
∠AOP=25°．
点评：本题考查了切线的性质及圆周角定理，同学们要学会由切线入手解决这类问题．
分析：连接OA，由PA是⊙O的切线，则∠OAP=90°，又∠P=40°，则∠AOP=50°，再由圆周角定理得出∠ACP的度数．
解答：
解：连接OA．由于PA是⊙O的切线，则△APO是直角三角形；
在Rt△APO中，∠P=40°，∠AOP=50°；
再由圆周角定理，∠ACP=
∠AOP=25°．点评：本题考查了切线的性质及圆周角定理，同学们要学会由切线入手解决这类问题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图，AB是⊙O的直径，点D在AB的延长线上，过点D作⊙O的切线，切点为C，若∠A=35°，则∠D=
如图，AC是⊙O的直径，BD是⊙O的弦，EC∥AB，交⊙O于E．图中与∠BOC的一半相等的角有
如图，AB是⊙O的直径，D为弧AC的中点，∠B=50°，则∠DAC=
如图，AB是⊙O的直径，∠ABC=30°，OA=2，则BC长为
如图：P是⊙O的直径BA延长线上一点，PD交⊙O于点C，且PC=OD，如果∠P=24°，则∠DOB=