题目内容
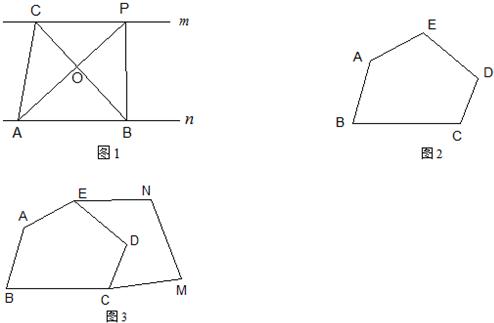
如图1和图2，有多个长方形和正方形的卡片，图1是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．根据图2，利用面积的不同表示方法，写出一个代数恒等式________．
（a+b）（a+2b）=a2+2b2+3ab
分析：表示阴影部分的面积有两种方法：①大长方形的面积=（a+b）（a+2b），②3个正方形的面积加上3个矩形的面积a2+ab+ab+ab+b2+b2，推出即可．
解答：由图2可知：阴影部分的面积是：①（a+b）（a+2b），②a2+ab+ab+ab+b2+b2=a2+2b2+3ab，
∴（a+b）（a+2b）=a2+2b2+3ab，
故答案为：（a+b）（a+2b）=a2+2b2+3ab．
点评：本题考查了完全平方公式的几何背景的应用，关键是检查学生能否正确表示图形中阴影部分的面积，题目具有一定的代表性，考查了学生的理解能力、观察图形的能力等
分析：表示阴影部分的面积有两种方法：①大长方形的面积=（a+b）（a+2b），②3个正方形的面积加上3个矩形的面积a2+ab+ab+ab+b2+b2，推出即可．
解答：由图2可知：阴影部分的面积是：①（a+b）（a+2b），②a2+ab+ab+ab+b2+b2=a2+2b2+3ab，
∴（a+b）（a+2b）=a2+2b2+3ab，
故答案为：（a+b）（a+2b）=a2+2b2+3ab．
点评：本题考查了完全平方公式的几何背景的应用，关键是检查学生能否正确表示图形中阴影部分的面积，题目具有一定的代表性，考查了学生的理解能力、观察图形的能力等
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
【倾听理解】（这是一次数学活动课上，师生利用“几何画板”软件探究函数性质的活动片段）