题目内容
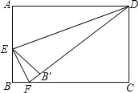
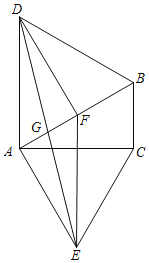
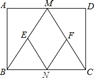
【题目】已知：如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是线段BM、CM的中点．
（1）求证：△ABM≌△DCM；
（2）填空：当AB：AD= 时，四边形MENF是正方形．
【答案】（1）见解析；（2）当AB：AD=1：2时，四边形MENF是正方形．
【解析】
（1）根据矩形性质得出AB=DC，∠A=∠D=90°，根据全等三角形的判定推出即可；
（2）求出四边形MENF是平行四边形，求出∠BMC=90°和ME=MF，根据正方形的判定推出即可．
（1）∵四边形ABCD是矩形，∴AB=DC，∠A=∠D=90°．
∵M为AD的中点，∴AM=DM．
在△ABM和△DCM中，∵
，∴△ABM≌△DCM（SAS）．
（2）当AB：AD=1：2时，四边形MENF是正方形．理由如下：
∵AB：AD=1：2，AM=DM，AB=CD，∴AB=AM=DM=DC．
∵∠A=∠D=90°，∴∠ABM=∠AMB=∠DMC=∠DCM=45°，∴∠BMC=90°．
∵四边形ABCD是矩形，∴∠ABC=∠DCB=90°，∴∠MBC=∠MCB=45°，∴BM=CM．
∵N、E、F分别是BC、BM、CM的中点，∴BE=CF，ME=MF，NF∥BM，NE∥CM，∴四边形MENF是平行四边形．
∵ME=MF，∠BMC=90°，∴四边形MENF是正方形，即当AB：AD=1：2时，四边形MENF是正方形．
故答案为：1：2．
【题目】惠民新村分给小慧家一套价格为12万元的住房.按要求，需首期(第一年)付房款3万元，从第二年起，每年应付房款0.5万元与上一年剩余房款的利息的和.假设剩余房款年利率为0.4%，小慧列表推算如下：
第一年 | 第二年 | 第三年 | … | |
应还款（万元） | 3 |
|
| … |
剩余房款（万元） | 9 | 8.5 | 8 | … |
若第
年小慧家仍需还款，则第年应还款_______万元(＞1).
