题目内容
 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).(1)求出图象与x轴的交点A,B的坐标;
(2)设抛物线与y轴交于点C,求△BCM的面积.
(3)在图中的抛物线上是否还存在点P,使得S△PMB=S△BCM?如果不存在,说明理由;如存在,请直接写出P点的个数.
【答案】分析:(1)所给二次函数解析式是顶点式,而顶点坐标是(1,-4),易求m、k的值,再把所求m、k的值代入二次函数中,令y=0,解关于x的一元二次方程,可求x=3或x=-1,进而可得A、B的坐标;
(2)令二次函数中的x=0,易求y=-3,从而可得C点坐标(0,-3),由于B、C、M三点坐标都是已知的,根据两点之间的距离公式,易求BC= ,BM=
,BM= ,CM=
,CM= ,而BC2+CM2=BM2,根据勾股定理逆定理可知△BCM是直角三角形,进而可求其面积;
,而BC2+CM2=BM2,根据勾股定理逆定理可知△BCM是直角三角形,进而可求其面积;
(3)根据同底等高的三角形面积相等,那么过点C作BM的平行线,观察可知与抛物线有2个交点,故P点的个数是2.
解答:解:(1)根据题意,可得-m=1,k=-4,
解得m=-1,k=-4,
把m=-1,k=-4代入函数解析式,得
y=(x-1)2-4,
令y=0,得(x-1)2-4=0,
解得x=3或x=-1,
∴A点坐标是(-1,0),B点坐标是(3,0);
 (2)令x=0,得y=-3,
(2)令x=0,得y=-3,
∴抛物线和y轴的交点C的坐标是(0,-3),
∵B(3,0),C(0,-3),M(1,-4),
∴BC= ,BM=
,BM= ,CM=
,CM= ,
,
∴BC2+CM2=BM2,
∴△BCM是直角三角形,
∴S△BCM= ×
× ×
× =3;
=3;
(3)过点C作BM的平行线,可观察与抛物线有两个交点,
故点P的个数是2.
点评:本题考查了二次函数综合题,解题关键是注意掌握二次函数顶点式的表示方法,以及求任意三角形面积时,要先考虑是否是直角三角形,同底等高的三角形面积相等.
(2)令二次函数中的x=0,易求y=-3,从而可得C点坐标(0,-3),由于B、C、M三点坐标都是已知的,根据两点之间的距离公式,易求BC=
 ,BM=
,BM= ,CM=
,CM= ,而BC2+CM2=BM2,根据勾股定理逆定理可知△BCM是直角三角形,进而可求其面积;
,而BC2+CM2=BM2,根据勾股定理逆定理可知△BCM是直角三角形,进而可求其面积;(3)根据同底等高的三角形面积相等,那么过点C作BM的平行线,观察可知与抛物线有2个交点,故P点的个数是2.
解答:解:(1)根据题意,可得-m=1,k=-4,
解得m=-1,k=-4,
把m=-1,k=-4代入函数解析式,得
y=(x-1)2-4,
令y=0,得(x-1)2-4=0,
解得x=3或x=-1,
∴A点坐标是(-1,0),B点坐标是(3,0);
 (2)令x=0,得y=-3,
(2)令x=0,得y=-3,∴抛物线和y轴的交点C的坐标是(0,-3),
∵B(3,0),C(0,-3),M(1,-4),
∴BC=
 ,BM=
,BM= ,CM=
,CM= ,
,∴BC2+CM2=BM2,
∴△BCM是直角三角形,
∴S△BCM=
 ×
× ×
× =3;
=3;(3)过点C作BM的平行线,可观察与抛物线有两个交点,
故点P的个数是2.
点评:本题考查了二次函数综合题,解题关键是注意掌握二次函数顶点式的表示方法,以及求任意三角形面积时,要先考虑是否是直角三角形,同底等高的三角形面积相等.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 16、如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=mx+n(m≠0)的图象,当y2>y1,x的取值范围是
16、如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=mx+n(m≠0)的图象,当y2>y1,x的取值范围是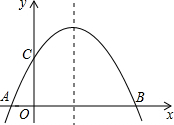 如图是二次函数y=2x2-4x-6的图象,那么方程2x2-4x-6=0的两根之和
如图是二次函数y=2x2-4x-6的图象,那么方程2x2-4x-6=0的两根之和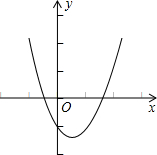 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①c>0;②a+b+c<0;③2a-b<0;④b2+8a>4ac中正确的是(填写序号)
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①c>0;②a+b+c<0;③2a-b<0;④b2+8a>4ac中正确的是(填写序号) 如图是二次函数
如图是二次函数 如图是二次函数y=ax2+bx+c的部分图象,由图象可知方程ax2+bx+c=0的解是
如图是二次函数y=ax2+bx+c的部分图象,由图象可知方程ax2+bx+c=0的解是