题目内容
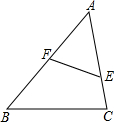 如图,△ABC中,F、E分别是AB,AC上的点,当________时(请添加一个条件)使△AFE与△ABC相似.
如图,△ABC中,F、E分别是AB,AC上的点,当________时(请添加一个条件)使△AFE与△ABC相似.
此题答案不唯一,如∠AEF=∠B或∠AFE=∠C或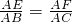 或AE•AC=AB•AF等
或AE•AC=AB•AF等
分析:首先由图可得∠A是公共角,然后根据有两角对应相等的三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似,可求得答案.
解答:∵∠A是公共角,
∴当∠AEF=∠B或∠AFE=∠C时,利用有两角对应相等的三角形相似,可判定△AEF∽△ABC;
当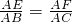 或AE•AC=AB•AF时,利用两组对应边的比相等且夹角对应相等的两个三角形相似,可判定△AEF∽△ABC.
或AE•AC=AB•AF时,利用两组对应边的比相等且夹角对应相等的两个三角形相似,可判定△AEF∽△ABC.
此题答案不唯一,当添加∠AEF=∠B或∠AFE=∠C或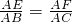 或AE•AC=AB•AF等,可使得△AFE与△ABC相似.
或AE•AC=AB•AF等,可使得△AFE与△ABC相似.
故答案为:此题答案不唯一,如∠AEF=∠B或∠AFE=∠C或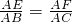 或AE•AC=AB•AF等.
或AE•AC=AB•AF等.
点评:此题考查了相似三角形的判定.此题比较简单,注意熟练掌握相似三角形的判定定理是解此题的关键.
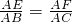 或AE•AC=AB•AF等
或AE•AC=AB•AF等分析:首先由图可得∠A是公共角,然后根据有两角对应相等的三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似,可求得答案.
解答:∵∠A是公共角,
∴当∠AEF=∠B或∠AFE=∠C时,利用有两角对应相等的三角形相似,可判定△AEF∽△ABC;
当
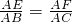 或AE•AC=AB•AF时,利用两组对应边的比相等且夹角对应相等的两个三角形相似,可判定△AEF∽△ABC.
或AE•AC=AB•AF时,利用两组对应边的比相等且夹角对应相等的两个三角形相似,可判定△AEF∽△ABC.此题答案不唯一,当添加∠AEF=∠B或∠AFE=∠C或
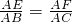 或AE•AC=AB•AF等,可使得△AFE与△ABC相似.
或AE•AC=AB•AF等,可使得△AFE与△ABC相似.故答案为:此题答案不唯一,如∠AEF=∠B或∠AFE=∠C或
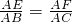 或AE•AC=AB•AF等.
或AE•AC=AB•AF等.点评:此题考查了相似三角形的判定.此题比较简单,注意熟练掌握相似三角形的判定定理是解此题的关键.

练习册系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.