题目内容
 23、如图,已知等腰直角三角形ABC中,∠ACB=Rt∠,AC=BC,顶点C在直线l上,分别过A,B作AD⊥l,BE⊥l,垂足分别为D,E两点,试探索AD,BE,DE三者间的关系,并证明.
23、如图,已知等腰直角三角形ABC中,∠ACB=Rt∠,AC=BC,顶点C在直线l上,分别过A,B作AD⊥l,BE⊥l,垂足分别为D,E两点,试探索AD,BE,DE三者间的关系,并证明.分析:有条件可判定△ADC≌△BCE,有全等三角形的性质可得:AD=CE,BE=CE,又因为DC+CE=DE所以AD+BE=DE.
解答:AD+BE=DE.
证明:∵∠ACB=90°
∴∠ACD+∠BCE=90°.
∵AD⊥l,BE⊥l,
∴∠ADC=∠BEC=90°,
∴∠ACD+∠CAD=90°,
∴∠BCE=∠ACD.
∵AC=BC,
∴△ADC≌△BCE.
∴AD=CE,BE=CE.
∵DC+CE=DE,
∴AD+BE=DE.
证明:∵∠ACB=90°
∴∠ACD+∠BCE=90°.
∵AD⊥l,BE⊥l,
∴∠ADC=∠BEC=90°,
∴∠ACD+∠CAD=90°,
∴∠BCE=∠ACD.
∵AC=BC,
∴△ADC≌△BCE.
∴AD=CE,BE=CE.
∵DC+CE=DE,
∴AD+BE=DE.
点评:本题考查了全等三角形的判定和性质,常用的判定方法为:SAS,SSS,AAS,ASA.常用到的性质是:对应角相等,对应边相等.

练习册系列答案
相关题目
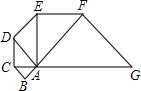 如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为
如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为 如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为
如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为 的直角边长为1,以Rt△
的直角边长为1,以Rt△ 为直角边,画第二个等腰直角三角形
为直角边,画第二个等腰直角三角形 ,再以Rt△
,再以Rt△ 为直角边,画第三个等腰直角三角形
为直角边,画第三个等腰直角三角形 ,…,以此类推;
,…,以此类推;
 长是________________;
长是________________; 个等腰直角三角形的斜边
个等腰直角三角形的斜边 长是________________;(用含
长是________________;(用含 的直角边长为1,以Rt△
的直角边长为1,以Rt△ 为直角边,画第二个等腰直角三角形
为直角边,画第二个等腰直角三角形 ,再以Rt△
,再以Rt△ 为直角边,画第三个等腰直角三角形
为直角边,画第三个等腰直角三角形 ,…,以此类推;
,…,以此类推;
 长是________________;
长是________________; 个等腰直角三角形的斜边
个等腰直角三角形的斜边 长是________________;(用含
长是________________;(用含