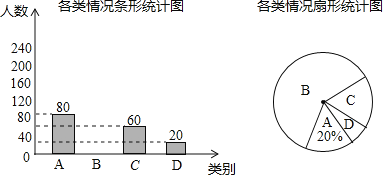
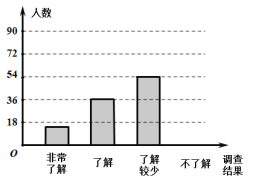
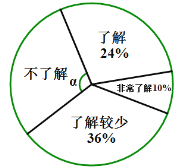
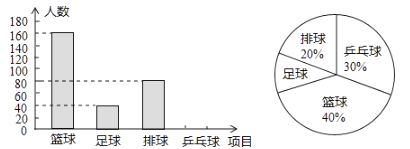
��Ŀ����
����Ŀ���Ķ�������ϣ�
�Ͽ�ʱ����ʦ�������һ�����⣺��������ʵ��![]() ������
������![]() �IJ���ʽ
�IJ���ʽ![]() ���������
���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
С����˼·�ǣ�ԭ����ʽ�ȼ���![]() ���躯��
���躯��![]() ��
��![]() ����������������ͼ���ʾ��ͼ������ԭ����ת��Ϊ����
����������������ͼ���ʾ��ͼ������ԭ����ת��Ϊ����![]() ��ͼ����
��ͼ����![]() ��ͼ���Ϸ�ʱ
��ͼ���Ϸ�ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��

����С����˼·�ش�
��������ʵ��![]() ������
������![]() �IJ���ʽ
�IJ���ʽ![]() ���������
���������![]() ��ȡֵ��Χ��_____��
��ȡֵ��Χ��_____��
�ο�С��˼������ķ�����������⣺
����![]() �ķ���
�ķ���![]() ��
��![]() ��Χ���������⣬��
��Χ���������⣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡����С����˼·�ش�a��-2��������⣺-2��b��2��
��������
���С����˼·�ش𣺸��ݶ��κ����������꼴�ɵ�a��ȡֵ��Χ��
������⣺ԭ���̿�ת��Ϊx2-4x+2=b����y1=x2-4x+2��y2=b���Ǻ���y1��![]() �ڵ�ͼ��ΪG��ԭ����ת��Ϊy2=b��G����������ʱ��b��ȡֵ��Χ�����ͼ�ɵô𰸣�
�ڵ�ͼ��ΪG��ԭ����ת��Ϊy2=b��G����������ʱ��b��ȡֵ��Χ�����ͼ�ɵô𰸣�
���С����˼·�ش���ͼ���֪��a��-2ʱ������x�IJ���ʽx2-2x-1-a��0�������
�ʴ�Ϊ��a��-2��

������⣺ԭ���̿�ת��Ϊx2-4x+2=b����y1=x2-4x+2��y2=b���Ǻ���y1��![]() �ڵ�ͼ��ΪG��
�ڵ�ͼ��ΪG��
��ͼ���֪����y2=b��G����������ʱ��b��ȡֵ��ΧΪ-2��b��2��


��ϰ��ϵ�д�
 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
�����Ŀ