题目内容
已知△ABC中，BC=6，AB=8，AC=10，O为三条角平分线的交点，则O到各边的距离为________．
2
分析：先判定△ABC为直角三角形，根据角平分线的性质定理解答．
解答：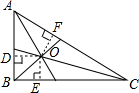
解：因为BC=6，AC=8，AC=10，所以BC2+AB2=36+64=100=AC2，根据勾股定理的逆定理，△ABC为直角三角形．根据角平分线的性质，OD=OE=OF=r；则S△AOB+S△BOC+S△AOC=S△ABC，
即
×6r+×8r+×10r=×6×8，
解得r=2．
故填2．
点评：根据勾股定理的逆定理和角平分线的性质，用面积法解答．
分析：先判定△ABC为直角三角形，根据角平分线的性质定理解答．
解答：
解：因为BC=6，AC=8，AC=10，所以BC2+AB2=36+64=100=AC2，根据勾股定理的逆定理，△ABC为直角三角形．根据角平分线的性质，OD=OE=OF=r；则S△AOB+S△BOC+S△AOC=S△ABC，即
×6r+×8r+×10r=×6×8，解得r=2．
故填2．
点评：根据勾股定理的逆定理和角平分线的性质，用面积法解答．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知△ABC中，BC=6cm，E、F分别是AB、AC的中点，那么EF长是
如图，已知△ABC中，BC=13cm，AB=10cm，AB边上的中线CD=12cm，则AC的长是（ ）| A、13cm | ||
| B、12cm | ||
| C、10cm | ||
D、
|
如图，已知△ABC中，BC=18，E，F为BC的三等分点，AE=10，AF=8，G，H分别为AC，AB的中点，则四边形EFGH的周长为