题目内容
如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M、N.

(1)求线段OD的长;
(2)若tan∠C= ,求弦MN的长.
,求弦MN的长.
【答案】
(1)5;(2)4.
【解析】
试题分析:(1)根据CD∥AB可知,△OAB∽△OCD,再根据相似三角形的对应边成比例即可求出OD的长;
(2)过O作OE⊥CD,连接OM,由垂径定理可知ME= MN,再根据tan∠C=
MN,再根据tan∠C= 可求出OE的长,利用勾股定理即可求出ME的长,进而求出答案.
可求出OE的长,利用勾股定理即可求出ME的长,进而求出答案.
试题解析:(1)∵CD∥AB,∴∠OAB=∠OCD,∠OBA=∠ODC,∴△OAB∽△OCD,∴ ,即
,即 ,又OA=3,AC=2,∴OB=3,∴
,又OA=3,AC=2,∴OB=3,∴ ,∴OD=5;
,∴OD=5;
(2)过O作OE⊥CD,连接OM,则ME= MN,∵tan∠C=
MN,∵tan∠C= ,即
,即 =
= ,∴设OE=
,∴设OE= ,则CE=
,则CE= ,在Rt△OEC中,OC2=OE2+CE2,即
,在Rt△OEC中,OC2=OE2+CE2,即 ,解得
,解得 ,在Rt△OME中,OM2=OE2+ME2,即
,在Rt△OME中,OM2=OE2+ME2,即 ,解得ME=2.∴MN=4,∴弦MN的长为4.
,解得ME=2.∴MN=4,∴弦MN的长为4.

考点:1.垂径定理;2.勾股定理;3.相似三角形的判定与性质;4.解直角三角形.

练习册系列答案
相关题目
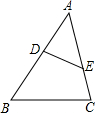 如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为
如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为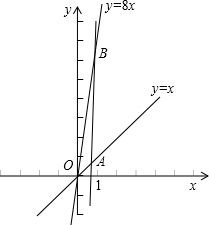 如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当
如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当 19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数.
19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数. 12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( ) 如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.
如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.