题目内容
16．不等式组$\left\{\begin{array}{l}{3-x＞0}\\{x＞-a}\end{array}\right.$无解，则a的取值范围是a≤-3．分析 首先解每个不等式求得每个不等式的解集，根据不等式组无解即可得到关于a的不等式，从而求得a范围．
解答 解：$\left\{\begin{array}{l}{3-x＞0…①}\\{x＞-a…②}\end{array}\right.$，
解①得x＜3，
根据题意得-a≥3，
解得：a≤-3．
故答案是：a≤-3．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
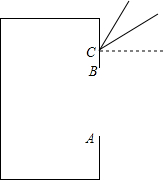某地在一年中阳光与地面的最大角为60°，最小角为30°，当地的某一新建住宅区的住户准备统一在向阳的一边设计统一高度的窗，并在这些窗上方做一块“遮阳蓬”，如图所示．已知窗的统一高度AB为2米，试用你所学的知识，计算“遮阳蓬”CD应从窗的上方多高的点C伸出，伸出多长才能使房间内“冬暖夏凉”？
在△ABC中，E、F分别为边AB、AC的中点，G为线段EF上一点，记△ABC、△AGC、△ABG、△GBC面积分别为S、S1、S2、S3，已知S1=λ1S，S2=λ2S，S3=λ3S，且λ3=2λ1，则$\frac{1}{λ_1}+\frac{2}{λ_2}+\frac{3}{λ_3}$=18．
4．下列化简正确的是（ ）
| A． | $\sqrt{27}$=9$\sqrt{3}$ | B． | $\sqrt{28}$=2$\sqrt{14}$ | C． | $\sqrt{\frac{7}{24}}$=$\frac{\sqrt{21}}{12}$ | D． | $\sqrt{\frac{3}{8}}$=$\frac{\sqrt{6}}{4}$ |
2015年5月中旬，中国和俄罗斯海军在地中海海域举行了代号为“海上联合-2015（1）”的联合军事演习，这是中国第一次地中海举行军事演习，也是这个海军距本土最远的一次军演，某天，“临沂舰”、“潍坊舰”两舰同时从A、B两个港口出发，均沿直线匀速驶向演习目标地海岛C，两舰艇都到达C岛后演习第一阶段结束，已知B刚位于A港、C岛之间，且A、B、C在一条直线上，如图所示，l临、l潍分别表示“临沂舰”、“潍坊舰”离B港的距离行驶时间x（h）变化的图象．