Question

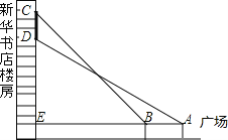
【题目】如图，小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD，点A是小刚的眼睛，测得屏幕下端D处的仰角为30°，然后他正对屏幕方向前进了6m到达B处，又测得该屏幕上端C处的仰角为45°，延长AB与楼房垂直相交于点E，测得BE=21m，则该屏幕上端与下端之间的距离CD为______m．

Answer 1

【答案】（21-9）．

【解析】

根据题意，利用锐角三角函数可以求得DE和CE的长，从而可以求得CD的长，本题得以解决．

∵BE=21m，AB=6m，

∴AE=AB+BE=27m，

∵∠DAE=30°，tan∠DAE=，

∴，

解得，DE=9，

∵∠CBE=45°，BE=21m，∠CEB=90°，

∴CE=BE=21m，

∴CD=CE-DE=（21-9）m，

故答案为：（21-9）．