题目内容
如图△ABC中，∠C=90°，⊙O分别切AC，BD于M，N，圆心O在AB上，⊙O的半径为12cm，BO=20cm，则AO的长是
- A.10cm
- B.8cm
- C.12cm
- D.15cm
D
分析：连接ON，OM，可证明四边形CMON为正方形，由△AOM∽△ABC，根据相似三角形的性质求得AO的长．
解答：
解：如图，连接ON，OM，
∴ON⊥BC，∴由勾股定理得BN2=BO2-ON2，
∵ON=12cm，BO=20cm，∴BN=16cm，
∴
，
即
=
，
解得AO=15cm，
故选D．
点评：本题考查了勾股定理、切线的性质、相似三角形的判定和性质，是基础知识要熟练掌握．
分析：连接ON，OM，可证明四边形CMON为正方形，由△AOM∽△ABC，根据相似三角形的性质求得AO的长．
解答：
解：如图，连接ON，OM，∴ON⊥BC，∴由勾股定理得BN2=BO2-ON2，
∵ON=12cm，BO=20cm，∴BN=16cm，
∴
，即
=，解得AO=15cm，
故选D．
点评：本题考查了勾股定理、切线的性质、相似三角形的判定和性质，是基础知识要熟练掌握．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
8、如图△ABC中，AB=3，AC=2，BO平分∠ABC，CO平分∠ACB．DE过点O交AB于D，交AC于E，且DE∥BC．则△ADE周长为
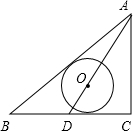如图△ABC中，∠C=90°，AC=6，AB=10，D是BC边的中点，以AD上一点O为圆心的圆与AB，BC都相切，则⊙O的半径为（ ）A、
| ||
B、
| ||
C、
| ||
| D、2 |
（2013•南岗区一模）如图△ABC中，DE∥BC，CD、BE交于点F，若DF=1，CF=3，AD=2，则线段BD的长等于
如图△ABC中，∠A=78°，AB=AC，P为△ABC内一点，连BP，CP，使∠PBC=9°，∠PCB=30°，连PA，则∠BAP的度数为
如图△ABC中，∠ABC=20°，外角∠ABF的平分线与CA边的延长线交于点D，外角∠EAC的平分线交BC边的延长线于点H，若∠BDA=∠DAB，则∠AHC=（ ）度．