题目内容
17.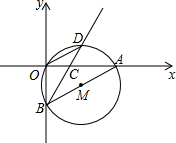 如图,在直角坐标系中,⊙M经过原点O(0,0),点A($\sqrt{6}$,0)与点B(0,-$\sqrt{2}$),点D在劣弧$\widehat{OA}$上,连接BD交x轴于点C,且∠COD=∠CBO.
如图,在直角坐标系中,⊙M经过原点O(0,0),点A($\sqrt{6}$,0)与点B(0,-$\sqrt{2}$),点D在劣弧$\widehat{OA}$上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.
分析 (1)由点A($\sqrt{6}$,0)与点B(0,-$\sqrt{2}$),可求得线段AB的长,然后由∠AOB=90°,可得AB是直径,继而求得⊙M的半径;
(2)由圆周角定理可得:∠COD=∠ABC,又由∠COD=∠CBO,即可得BD平分∠ABO;
(3)首先过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,易得△AEC是等边三角形,继而求得EF与AF的长,则可求得点E的坐标.
解答 解:(1)∵点A($\sqrt{6}$,0)与点B(0,-$\sqrt{2}$),
∴OA=$\sqrt{6}$,OB=$\sqrt{2}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$,
∵∠AOB=90°,
∴AB是直径,
∴⊙M的半径为:$\sqrt{2}$;
(2)∵∠COD=∠CBO,∠COD=∠CBA,
∴∠CBO=∠CBA,
即BD平分∠ABO;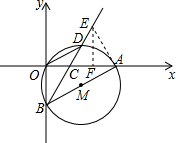 (3)如图,过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,即AE是切线,
(3)如图,过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,即AE是切线,
∵在Rt△AOB中,tan∠OAB=$\frac{OB}{OA}$=$\frac{\sqrt{2}}{\sqrt{6}}$=$\frac{\sqrt{3}}{3}$,
∴∠OAB=30°,
∴∠ABO=90°-∠OAB=60°,
∴∠ABC=∠OBC=$\frac{1}{2}$∠ABO=30°,
∴OC=OB•tan30°=$\sqrt{2}$×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{6}}{3}$,
∴AC=OA-OC=$\frac{2\sqrt{6}}{3}$,
∴∠ACE=∠ABC+∠OAB=60°,
∴∠EAC=60°,
∴△ACE是等边三角形,
∴AE=AC=$\frac{2\sqrt{6}}{3}$,
∴AF=$\frac{1}{2}$AE=$\frac{\sqrt{6}}{3}$,EF=$\frac{\sqrt{3}}{2}$AE=$\sqrt{2}$,
∴OF=OA-AF=$\frac{2\sqrt{6}}{3}$,
∴点E的坐标为:($\frac{2\sqrt{6}}{3}$,$\sqrt{2}$).
点评 此题属于圆的综合题,考查了勾股定理、圆周角定理、等边三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

 如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
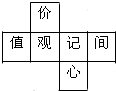 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )| A. | 记 | B. | 观 | C. | 心 | D. | 间 |
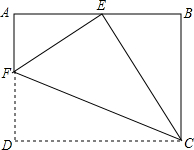 如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$.
如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$.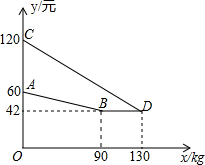 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.