题目内容
 如图,A、M是反比例函数图象上的两点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.BM:DM=8:9,当四边形OADM的面积为
如图,A、M是反比例函数图象上的两点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.BM:DM=8:9,当四边形OADM的面积为 时,k=________.
时,k=________.
6
分析:首先根据四边形OADM的面积为 ,BM:DM=8:9,及反比例系数k的几何意义求出△OBM的面积,从而得出k的值.
,BM:DM=8:9,及反比例系数k的几何意义求出△OBM的面积,从而得出k的值.
解答:∵MB∥x轴,AC∥y轴,
∴OBDC是矩形.
∵BM:DM=8:9,
∴BM:BD=8:17,
∴△OBM的面积:矩形OBDC的面积=4:17.
∵△OBM的面积=△OAC的面积
∴△OBM的面积:[矩形OBDC的面积-(△OBM的面积+△OAC的面积)]
=△OBM的面积:四边形OADM的面积
=4:9
∵四边形OADM的面积为 .
.
∴△OBM的面积=3
根据反比例系数k的几何意义可知k=6.
故答案为:6.
点评:本题考查反比例系数k的几何意义,图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S= |k|.该知识点是中考的重要考点,同学们应高度关注.
|k|.该知识点是中考的重要考点,同学们应高度关注.
分析:首先根据四边形OADM的面积为
 ,BM:DM=8:9,及反比例系数k的几何意义求出△OBM的面积,从而得出k的值.
,BM:DM=8:9,及反比例系数k的几何意义求出△OBM的面积,从而得出k的值.解答:∵MB∥x轴,AC∥y轴,
∴OBDC是矩形.
∵BM:DM=8:9,
∴BM:BD=8:17,
∴△OBM的面积:矩形OBDC的面积=4:17.
∵△OBM的面积=△OAC的面积
∴△OBM的面积:[矩形OBDC的面积-(△OBM的面积+△OAC的面积)]
=△OBM的面积:四边形OADM的面积
=4:9
∵四边形OADM的面积为
 .
.∴△OBM的面积=3
根据反比例系数k的几何意义可知k=6.
故答案为:6.
点评:本题考查反比例系数k的几何意义,图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=
 |k|.该知识点是中考的重要考点,同学们应高度关注.
|k|.该知识点是中考的重要考点,同学们应高度关注. 
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )
如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
 如图,A、B是反比例函数y=
如图,A、B是反比例函数y=| k |
| x |
| A、S△ADB>S△ACB |
| B、S△ADB<S△ACB |
| C、S△ADB=S△ACB |
| D、不确定 |
 如图所示,P是反比例函数
如图所示,P是反比例函数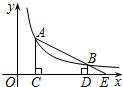 如图,A,B是反比例函数y=
如图,A,B是反比例函数y= 如图,若点P是反比例函数y=
如图,若点P是反比例函数y=