题目内容
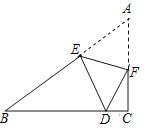
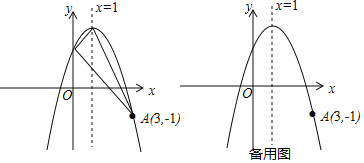
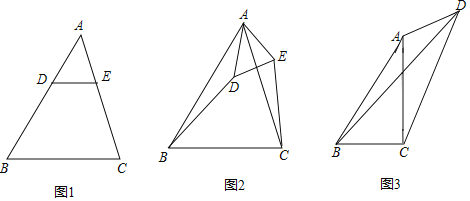
【题目】（1）如图1，在△ABC中，AB＞AC，点D，E分别在边AB，AC上，且DE∥BC，若AD＝2，AE＝
，则
的值是 ；
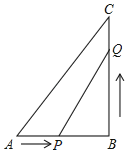
（2）如图2，在（1）的条件下，将△ADE绕点A逆时针方向旋转一定的角度，连接CE和BD，的值变化吗？若变化，请说明理由；若不变化，请求出不变的值；
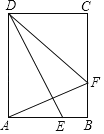
（3）如图3，在四边形ABCD中，AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝
，当CD＝6，AD＝3时，请直接写出线段BD的长度．
【答案】（1）
；（2）
的值不变化，值为，理由见解析；（3）
【解析】
（1）由平行线分线段成比例定理即可得出答案；
（2）证明△ABD∽△ACE，得出＝
＝
（3）作AE⊥CD于E，DM⊥AC于M，DN⊥BC于N，则DM＝CN，DN＝MC，由三角函数定义得出
＝，
＝，得出
＝
，求出AE＝AD＝
，DE＝AE＝
，得出CE＝CD﹣DE＝
，由勾股定理得出AC＝
＝
，得出BC＝AC＝
，由面积法求出CN＝DM＝
，得出BN＝BC+CN＝
，由勾股定理得出AM＝
＝
，得出DN＝MC＝AM+AC＝
，再由勾股定理即可得出答案．
（1）∵DE∥BC，
∴＝＝
＝；
故答案为：；
（2）的值不变化，值为；理由如下：
由（1）得：DE∥B，
∴△ADE∽△ABC，
∴
＝
，
由旋转的性质得：∠BAD＝∠CAE，
∴△ABD∽△ACE，
∴＝＝；
（3）作AE⊥CD于E，DM⊥AC于M，DN⊥BC于N，如图3所示：
则四边形DMCN是矩形，
∴DM＝CN，DN＝MC，
∵∠BAC＝∠ADC＝θ，且tanθ＝，
∴＝，＝，
∴＝，
∴AE＝AD＝×3＝，DE＝AE＝，
∴CE＝CD﹣DE＝6﹣＝，
∴AC＝＝
＝
∴BC＝AC＝，
∵△ACD的面积＝
AC×DM＝CD×AE，
∴CN＝DM＝
＝，
∴BN＝BC+CN＝，AM＝＝
＝，
∴DN＝MC＝AM+AC＝，
∴BD＝
＝
＝．
