Question

【题目】已知抛物线经过点A（1,0）和B（0,3），其顶点为D.

（1）求此抛物线的表达式；

（2）求△ABD的面积；

（3）设P为该抛物线上一点，且位于抛物线对称轴右侧，作PH⊥对称轴，垂足为H，若△DPH与△AOB相似，求点P的坐标.

Answer 1

【答案】（1）；（2）点P的坐标为（5,8），.

【解析】试题分析：（1）把A、B的坐标代入抛物线的解析式，解方程组即可；

（2）作DT⊥y轴于点T，由S△ABD= S△BTD -S△AOB-SOTDA计算即可；

（3）令P(p，p2-4p+3) (p＞2)．由△DPH与△AOB相似，易知∠AOB=∠PHD=90°，然后分两种情况讨论即可．

试题解析：解：（1）由题意得： ，

解得： ，

所以抛物线的表达式为．

（2）由（1）得D（2，﹣1），作DT⊥y轴于点T，

则△ABD的面积=．

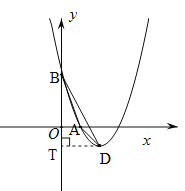
（3）令P．由△DPH与△AOB相似，易知∠AOB=∠PHD=90°，所以或，解得： 或，所以点P的坐标为（5，8），．