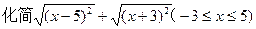题目内容
阅读材料,解答下列问题:求函数y=
| 2x+3 |
| x+1 |
解.∵y=
| 2x+3 |
| x+1 |
| 2(x+1)+1 |
| x+1 |
| 1 |
| x+1 |
∵
| 1 |
| x+1 |
∴y>2
在高中我们将学习这样一个重要的不等式:
| x+y |
| 2 |
| xy |
例如:求证:x+
| 1 |
| x |
证明:∵
x+
| ||
| 2 |
x•
|
∴x+
| 1 |
| x |
利用以上信息,解决以下问题:
(1)求函数:y=
| x+1 |
| x-1 |
(2)若x>0,求代数式2x+
| 4 |
| x |
分析:(1)中,y=
=
=1+
,再结合x>1,即可求出y的取值范围;
(2)中,2x+
=(
-
)2+4
≥4
.
| x+1 |
| x-1 |
| x-1+2 |
| x-1 |
| 2 |
| x-1 |
(2)中,2x+
| 4 |
| x |
| 2x |
|
| 2 |
| 2 |
解答:解:(1)y=1+
,
∵x>1,
∴x-1>0,
∴y>1.
(2)∵(
-
)2≥0,
∴(
)2-2
•
+(
)2≥0,
∴2x+
≥2
•
,
2x+
≥4
,
∴2x+
的最小值为4
.
| 2 |
| x-1 |
∵x>1,
∴x-1>0,
∴y>1.
(2)∵(
| 2x |
|
∴(
| 2x |
| 2x |
|
|
∴2x+
| 4 |
| x |
| 2x |
|
2x+
| 4 |
| x |
| 2 |
∴2x+
| 4 |
| x |
| 2 |
点评:此题是一道材料分析题,给出了求函数取值范围和最小值的方法.此题旨在考查同学们的阅读理解能力
和接受并应用新知识的能力,需对式子进行灵活变形,才能解决问题.
和接受并应用新知识的能力,需对式子进行灵活变形,才能解决问题.

练习册系列答案
相关题目
 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身 时,
时, ,故此时
,故此时 时,如
时,如 则
则 ,故此时
,故此时 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 的大小关系.
的大小关系.
 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身 时,
时, ,故此时
,故此时 时,如
时,如 则
则 ,故此时
,故此时 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 的大小关系.
的大小关系.