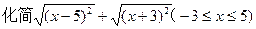题目内容
阅读材料,解答下列问题.例:当a>0时,如a=6,则|a|=|6|=6,故此时|a|是它本身;当a=0时,|a|=0,故此时|a|是零;
当a<0时,如a=-6,则|a|=|-6|=6=-(-6),故此时|a|是它的相反数.
综上所述,|a|可分三种情况,即|a|=
|
这种分析方法渗透了数学的分类讨论思想.
问:(1)请仿照例中的分类讨论的方法,分析二次根式
| a2 |
(2)猜想
| a2 |
| a2 |
(3)当1<x<2时,试化简:|x-1|+
| (x-2)2 |
分析:根据二次根式的性质解答.
解答:解:(1)当a>0时,如a=3,则
=
=3,故此时
的结果是它本身;
当a=0时,
=0,故此时
的结果是零;
当a<0时,如a=-3,则
=
=3=-(-3),故此时
的结果是它的相反数.
综上所述,
的结果可分三种情况,即
=
(2)
=|a|.
(3)∵1<x<2,
∴x-1>0,x-2<0,
∴|x-1|+
=x-1+(2-x)
=1.
| a2 |
| 32 |
| a2 |
当a=0时,
| a2 |
| a2 |
当a<0时,如a=-3,则
| a2 |
| (-3)2 |
| a2 |
综上所述,
| a2 |
| a2 |
|
(2)
| a2 |
(3)∵1<x<2,
∴x-1>0,x-2<0,
∴|x-1|+
| (x-2)2 |
=1.
点评:解答此题,要弄清以下问题:
①定义:一般地,形如
(a≥0)的代数式叫做二次根式.当a>0时,
表示a的算术平方根;当a=0时,
=0;当a<0时,二次根式无意义;
②性质:
=|a|.
①定义:一般地,形如
| a |
| a |
| 0 |
②性质:
| a2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身 时,
时, ,故此时
,故此时 时,如
时,如 则
则 ,故此时
,故此时 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 的大小关系.
的大小关系.
 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身 时,
时, ,故此时
,故此时 时,如
时,如 则
则 ,故此时
,故此时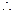 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 的大小关系.
的大小关系.