题目内容
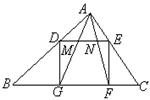
如图，△ABC中，∠BAC=90°，正方形的一边GF在BC上，其余两个顶点D，E分别在AB，AC上.连接AG，AF分别交DE于M，N两点．
(1)求证：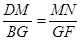
.
(2)求证：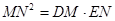
．
(3)若AB=AC=2，求MN的长.
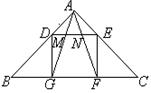
(1)求证：
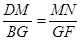.(2)求证：
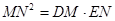．(3)若AB=AC=2，求MN的长.
（1）证明：∵四边形DGFE是正方形，∴DN∥BF，
∴△ADM∽△ABG，
∴
,同理可得
．
∴
．
（2）证明：
由（1）可知，同理也可以得到
,
∴
,
.
∵∠B＋∠C=90°，∠CEF＋∠C=90°．
∴∠B=∠CEF，
又∵∠BGD=∠EFC=Rt∠，
∴△BGD∽△EFC． ∴
.
∵DG,GF,EF是同一个正方形的边长，∴DG="GF=EF." ∴
∴
, ∴MN 2＝DM·EN
（3）MN=
∴△ADM∽△ABG，
∴
,同理可得． ∴
．（2）证明：
由（1）可知
，同理也可以得到,∴
,.∵∠B＋∠C=90°，∠CEF＋∠C=90°．
∴∠B=∠CEF，
又∵∠BGD=∠EFC=Rt∠，
∴△BGD∽△EFC． ∴
.∵DG,GF,EF是同一个正方形的边长，∴DG="GF=EF." ∴
∴
, ∴MN 2＝DM·EN （3）MN=
（1）通过三角形相似，证明线段之比相等；
（2） ∵
∴
∵∠B=∠C＝45o , 四边形DEFG是正方形，
∴
∵ 由（1）(2)可得
∴
（2） ∵
∴ ∵∠B=∠C＝45o , 四边形DEFG是正方形，
∴
∵ 由（1）(2)可得
∴
练习册系列答案
相关题目
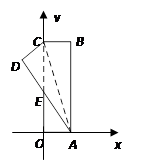
（顶点均在格点上），若它们是以P点为位似中心的位似图形，则P点的坐标是（ ）.
，
）
，
）
，
，
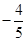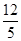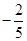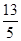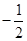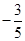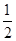BC．（要求保留作图痕迹，不必写出作法）