题目内容
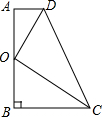 (2012•随州)如图:已知直角梯形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(2012•随州)如图:已知直角梯形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8cm,OD=6cm,求CD的长.
分析:(1)过O作OE垂直于CD,根据梯形的面积公式表示出梯形ABCD的面积,由O为AB的中点,将AB换为2OA,变形得到梯形的面积等于三角形OAD与三角形OBC的面积之和的2倍,又梯形ABCD的面积=三角形AOD的面积+三角形BOC的面积+三角形COD的面积,得到三角形COD的面积=三角形AOD的面积+三角形BOC的面积,而三角形AOD与三角形BOC都为直角三角形,三角形COD的面积等于CD乘以OE除以2,分别利用三角形的面积公式表示后,根据AD+BC=CD,得到OA=OE,又OA为圆O的半径,故得到CD过半径OE的端点E,且与半径OE垂直,进而确定出CD为圆O的切线;
(2)取CD的中点F,连接OF,又O为AB的中点,得到OF为梯形的中位线,利用梯形中位线定理得到OF等于上下底之和的一半,再利用AD+BC=CD变形,得到OF为CD的一半,即OF等于以CD为直径的圆F的半径,根据直径所对的圆周角为直角得到∠DOC为直角,在直角三角形COD中,由OD与OC的长,利用勾股定理即可求出CD的长.
(2)取CD的中点F,连接OF,又O为AB的中点,得到OF为梯形的中位线,利用梯形中位线定理得到OF等于上下底之和的一半,再利用AD+BC=CD变形,得到OF为CD的一半,即OF等于以CD为直径的圆F的半径,根据直径所对的圆周角为直角得到∠DOC为直角,在直角三角形COD中,由OD与OC的长,利用勾股定理即可求出CD的长.
解答:解:(1)过AB的中点O作OE⊥CD于E,
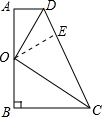
∵S梯形ABCD=
(AD+BC)•AB=(AD+BC)•OA=2(
AD•OA+
BC•OB)=2(S△OAD+S△OBC),
且S梯形ABCD=S△OBC+S△OAD+S△OCD,
∴S△OBC+S△OAD=S△OCD,且OA=OB,
∴
AD•OA+
BC•OB=
AD•OA+
BC•OA=
(AD+BC)•OA=
CD•OE,
又∵AD+BC=CD,
∴OA=OE,
∴E点在以AB为直径的⊙O上,又OE⊥CD,
∴CD是⊙O的切线,即CD与⊙O相切;
(2)在CD上取中点F,连接OF,
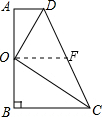
∵OF为梯形ABCD的中位线,且AD+BC=CD,
∴OF=
(AD+BC)=
CD,
∴O点在以CD为直径的⊙F上,
∴∠COD=90°,
在Rt△COD中,OD=6cm,OC=8cm,
∴根据勾股定理得:CD=
=
=10cm.

∵S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
且S梯形ABCD=S△OBC+S△OAD+S△OCD,
∴S△OBC+S△OAD=S△OCD,且OA=OB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵AD+BC=CD,
∴OA=OE,
∴E点在以AB为直径的⊙O上,又OE⊥CD,
∴CD是⊙O的切线,即CD与⊙O相切;
(2)在CD上取中点F,连接OF,

∵OF为梯形ABCD的中位线,且AD+BC=CD,
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
∴O点在以CD为直径的⊙F上,
∴∠COD=90°,
在Rt△COD中,OD=6cm,OC=8cm,
∴根据勾股定理得:CD=
| OD2+OC2 |
| 62+82 |
点评:此题考查了切线的性质与判定,勾股定理,梯形的中位线定理,以及梯形、三角形面积的计算,其中作出相应的辅助线是解本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 (2012•随州)如图,AB是⊙O的直径,若∠BAC=35°,则∠ADC=( )
(2012•随州)如图,AB是⊙O的直径,若∠BAC=35°,则∠ADC=( ) (2012•随州)如图,直线l与反比例函数y=
(2012•随州)如图,直线l与反比例函数y= (2012•随州)如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(2012•随州)如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.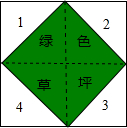 (2012•随州)如图所示,一个大正方形地面上,编号为1,2,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪,一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上.
(2012•随州)如图所示,一个大正方形地面上,编号为1,2,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪,一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上.