题目内容

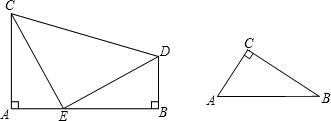
求下列图形中∠CDE=________．

40°
分析：首先由四边形的内角和定理求出∠ADC的度数，然后根据邻补角的定义求出∠CDE的大小．
解答：∵∠ADC=360°-90°-60°-70°=140°，
∴∠CDE=180°-140°=40°．
点评：本题主要考查了四边形的内角和定理及邻补角的定义．
四边形的内角和为360°，互为邻补角的两个角的和为180°．

练习册系列答案

新课标新精编系列答案

综合素质随堂反馈系列答案

目标复习检测卷系列答案

金种子领航考卷系列答案

领航1卷通系列答案

名校全优考卷单元夺冠100分系列答案

一卷通AB卷快乐学习夺冠100分系列答案

创新名校秘题系列答案

名校练加考系列答案

小学教材全测系列答案

相关题目

20、求下列图形中∠CDE=

如图，已知：AC⊥AB，BD⊥AB，且AC=BE，AE=BD，求证：△CDE是等腰直角三角形．
证明：∵AC⊥AB，BD⊥AB∴∠CAE=∠DBE=90°
∵AC=BE，AE=BD∴△ACE≌△BED
∴CE=DE且∠ACE=∠BED
∵∠ACE+∠AEC=90°∴∠AEC+∠BED=90°
∴∠CED=90°∴△CED为等腰直角三角形
利用上题的解题思路解答下列问题：
在Rt△ABC中，∠C=90°，D，E分别为CB，CA延长线上的点，BE与AD的交点为P．
（1）若BD=AC，AE=CD，在下图中画出符合题意的图形，求出∠APE的度数；
（2）若AC=

AE，则∠APE=

如图，已知：AC⊥AB，BD⊥AB，且AC=BE，AE=BD，求证：△CDE是等腰直角三角形；

证明：∵AC⊥AB，BD⊥AB   ∴∠CAE=∠DBE=90°
∵AC= BE，AE=BD    ∴△ACE≌△BED
∴CE=DE且∠ACE=∠BED
∵∠ACE+∠AEC=90° ∴∠AEC+∠BED=90°
∴∠CED=90°        ∴△CED为等腰直角三角形
利用上题的解题思路解答下列问题：
在Rt△ABC中，∠C=90°，D，E分别为CB，CA延长线上的点，BE与AD的交点为P.
【小题1】若BD=AC，AE=CD，在下图中画出符合题意的图形，求出∠APE的度数；
【小题2】若AC=BD，CD=AE，则∠APE=__________°

如图，已知：AC⊥AB，BD⊥AB，且AC=BE，AE=BD，求证：△CDE是等腰直角三角形；

证明：∵AC⊥AB，BD⊥AB ∴∠CAE=∠DBE=90°

∵AC= BE，AE=BD ∴△ACE≌△BED

∴CE=DE且∠ACE=∠BED

∵∠ACE+∠AEC=90° ∴∠AEC+∠BED=90°

∴∠CED=90° ∴△CED为等腰直角三角形

利用上题的解题思路解答下列问题：

在Rt△ABC中，∠C=90°，D，E分别为CB，CA延长线上的点，BE与AD的交点为P.

1.若BD=AC，AE=CD，在下图中画出符合题意的图形，求出∠APE的度数；

2.若AC=BD，CD=AE，则∠APE=__________°