题目内容
【题目】在平面直角坐标系中,已知抛物线![]() .
.
(1)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“方点”.试求拋物线![]() 的“方点”的坐标;
的“方点”的坐标;
(2)如图,若将该抛物线向左平移1个单位长度,新抛物线与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 左侧),与
左侧),与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() .若点
.若点![]() 是直线
是直线![]() 上方抛物线上的一点,求
上方抛物线上的一点,求![]() 的面积的最大值;
的面积的最大值;
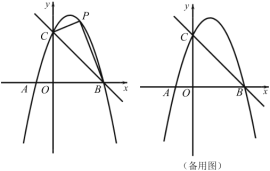
(3)第(2)问中平移后的抛物线上是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,直接写出所有符合条件的点
为直角边的直角三角形?若存在,直接写出所有符合条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)抛物线的方点坐标是![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)由定义得出x=y,直接代入求解即可
(2)作辅助线PD平行于y轴,先求出抛物线与直线的解析式,设出点P的坐标,利用点坐标求出PD的长,进而求出面积的二次函数,再利用配方法得出最大值
(3)通过抛物线与直线的解析式可求出点B,C的坐标,得出△OBC为等腰直角三角形,过点C作![]() 交x轴于点M,作
交x轴于点M,作![]() 交y轴于点N,得出M,N的坐标,得出直线BN、MC的解析式然后解方程组即可.
交y轴于点N,得出M,N的坐标,得出直线BN、MC的解析式然后解方程组即可.
解:(1)由题意得:![]() ∴
∴![]()
解得![]() ,
,![]()
∴抛物线的方点坐标是![]() ,
,![]() .
.
(2)过![]() 点作
点作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() .
.
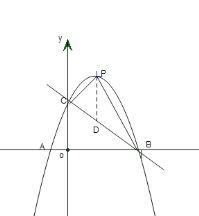
易得平移后抛物线的表达式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() .
.
设![]() ,则
,则![]() .
.
∴![]()
![]()
∴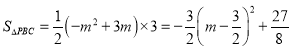
![]()
∴当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
(3)如图所示,过点C作![]() 交x轴于点M,作
交x轴于点M,作![]() 交y轴于点N
交y轴于点N
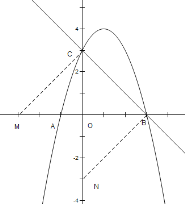
由已知条件得出点B的坐标为B(3,0),C的坐标为C(0,3),
∴△COB是等腰直角三角形,
∴可得出M、N的坐标分别为:M(-3,0),N(0,-3)
直线CM的解析式为:y=x+3
直线BN的解析式为:y=x-3
由此可得出: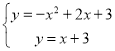 或
或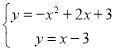
解方程组得出:![]() 或
或![]()
∴![]() 或
或![]()

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目