在△ABC中.∠ACB=90°.AC=BC.直线MN经过点C.且AD⊥MN于D.BE⊥MN于E．(1)当直线MN绕点C旋转到图1的位置时.求证:DE=AD+BE,(2)当直线MN绕点C旋转到图2的位置时.(1)中的结论还成立吗?若成立.请给出证明,若不成立.请写出新的结论并说明理由． DE=AC-BE [解析]试题分析:(1)利用等腰直角三角形.AC=B 题目和参考答案——青夏教育精英家教网——

题目内容

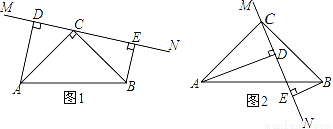
在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

（1）当直线MN绕点C旋转到图1的位置时，求证：DE=AD+BE；

（2）当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，请写出新的结论并说明理由．

（1）证明见解析；（2）DE=AC-BE 【解析】试题分析：（1）利用等腰直角三角形，AC=BC,再利用AAS得到△ADC和△CEB全等， DE=DC+CE=AD+BE. （2）利用等腰三角形得AC=BC,互余角性质得∠BCE=∠MAD,最后利用AAS得到△ADC和△CEB全等，DE=EC-CD=AD-BE．试题解析：证明：（1）∵AD⊥DE，BE⊥DE， ∴∠ADC...

练习册系列答案

世纪百通主体课堂小学课时同步达标系列答案

世纪百通优练测系列答案

世纪百通课时作业系列答案

百分学生作业本题练王系列答案

小学1课3练培优作业本系列答案

中华题王系列答案

优翼学练优系列答案

优加学习方案系列答案

52045模块式全能训练系列答案

钟书金牌新教材全练系列答案

相关题目

一列快车由甲地开往乙地，一列慢车由乙地开往甲地,两车同时出发, 匀速运动. 快车离乙地的路程y1(km) 与行驶的时间x(h) 之间的函数关系, 如图中线段AB 所示；慢车离乙地的路程y2(km) 与行驶的时间x(h)之间的函数关系, 如图中线段OC 所示。根据图象下列问题：

(1) 甲、乙两地之间的距离为__________km ；

(2) 线段AB 的解析式为_______________________；线段OC 的解析式为_________________________；

(3) 设快、慢车之间的距离为y(km), 求y 与慢车行驶时间x(h) 的函数关系式, 并画出函数的图象。

（1）450km（2）y1=﹣150x+450，y2=75x（3）答案见解析【解析】试题分析：（1）利用A点坐标为（0，450），可以得出甲，乙两地之间的距离；（2）利用A点坐标为（0，450），B点坐标为（3，0），代入y1=kx+b求出即可，利用线段OC解析式为y2="ax" 求出a即可；（3）利用（2）中所求得出，y=|y1-y2|进而求出函数解析式，得出图象即可． ...

若两数之和为负数，则下列叙述正确的是（）．

A. 两个都是负数 B. 这两个数不可能有正数

C. 两个数不可能有 D. 至少有一个负数

D 【解析】若两数之和为负数，则两数有可能为两负，一负一零，一负一正．故选．

若x1=﹣1是关于x的方程x2+mx﹣5=0的一个根，则方程的另一个根x2=__．

5 【解析】试题分析：首先将x=－1代入方程求出m的值，然后再去解关于x的一元二次方程．

关于x的一元二次方程ax2﹣x+1=0有实数根，则a的取值范围是（）

A. a≤且a≠0 B. a≤ C. a≥且a≠0 D. a≥

D 【解析】试题分析：根据一元二次方程的概念，可知a≠0，根据一元二次方程根的判别式，由方程有实数根，可求△=b2-4ac=（-1）2-4a≥0，解得a≤. 故选：A.

如图，在8×6正方形方格中，点A、B、C在小正方形的顶点上．

（1）在图中画出与△ABC关于直线成轴对称的△AB′C′，并回答问题：

图中线段CC′被直线l ；

（2）在直线l上找一点D，使线段DB+DC最短．（不写作法，应保留作图痕迹）

（3）在直线l确定一点P，使得|PA-PB|的值最小．（不写作法，应保留作图痕迹）

（1）详见解析；（2）详见解析；(3) 详见解析. 【解析】试题分析：（1）根据网格结构找出点B、C关于直线l的对称点B′、C′的位置，然后顺次连接即可，根据轴对称的性质，对称轴垂直平分对称点的连线；（2）根据轴对称确定最短路线，连接B′C，与对称轴l的交点即为所求点D；（3）作线段AB的中垂线EF交直线l于点P，则PA=PB，即|PA-PB|=0最短．试题解析：【解...

如图，一根长为30cm、宽为3 cm的长方形纸条，将它按图所示的过程折叠，为了美观，希望折叠完成后的纸条A端到点P的距离等于B端到点M的距离，则最初折叠时，MA的长应为__________cm．

10.5．【解析】将折叠这条展开如图，根据折叠的性质可知，两个梯形的上底等于纸条宽，即3cm，下底等于纸条宽的2倍，即6cm，两个三角形都为等腰直角三角形，斜边为纸条宽的2倍，即6cm，故超出点P的长度为（30-15）÷2=7.5， AM=7.5+3=10.5，故答案为：10.5.

如图，在等边中，，点、、分别在三边、、上，且，，，则的长为__________．

3 【解析】∵，， ∴， ∵为等边三角形， ∴， ∴， ∴， ∴． ∵， ∴， ∴， ∵，， ∴， ∴， ∵，， ∴， ∴， ∴．

如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（　　）

A. 44° B. 60° C. 67° D. 77°

C 【解析】试题分析：由∠ACB=90°，∠A=22°，三角形内角和是180º，可得∠B=90º-22º=68º，因为折叠角相等，所以∠CED=∠B=68º，∠BDC=∠EDC=∠BDE，，因为四边形内角和是360º，所以∠BDE=360º-90º-68º-68º=134º，所以∠BDC=∠BDE=×134º=67º．故选C．