题目内容
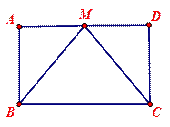
如图，菱形ABCD的对角线长分别为
，以菱形ABCD各边的中点为顶点作矩形A1B1C1D1，然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2，……，如此下去，得到四边形A2011B2011C2011D2011的面积用含的代数式表示为 ____。
，以菱形ABCD各边的中点为顶点作矩形A1B1C1D1，然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2，……，如此下去，得到四边形A2011B2011C2011D2011的面积用含的代数式表示为 ____。
根据三角形中位线定理，逐步推理出各小长方形的面积，总结出规律，用规律解答．
解：在2009个四边形中，小矩形有2008÷2+1=1005个，根据三角形中位线定理得：
第1个小矩形的面积为
a×b；
第2个小矩形的面积为（）2a×（）2b；
第3个小矩形的面积为（）3a×（）3b；
第4个小矩形的面积为（）4a×（）4b；
…
∴四边形A2011B2011C2011D2011的面积即为：第1007个小矩形的面积（）1006a×（）1006b=（）2012ab．
解：在2009个四边形中，小矩形有2008÷2+1=1005个，根据三角形中位线定理得：
第1个小矩形的面积为
a×b；第2个小矩形的面积为（
）2a×（）2b；第3个小矩形的面积为（
）3a×（）3b；第4个小矩形的面积为（
）4a×（）4b；…
∴四边形A2011B2011C2011D2011的面积即为：第1007个小矩形的面积（
）1006a×（）1006b=（）2012ab．
练习册系列答案
相关题目
中，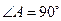
，
，
，另有一等腰梯形
（
）的底边
与
重合，两腰分别落在AB、AC上，且G、F分别是AB、AC的中点．
，将等腰梯形
与点
重合时停止．设运动时间为
秒，运动后的等腰梯形为
（如图2）．
能否是菱形？若能，请求出此时
，求
。
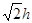