题目内容
在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB于E,若四边形ABCD的面积为8,则DE=( )
A、2
| ||
| B、3 | ||
C、3
| ||
D、
|
分析:可过点C作CF⊥DE,得出Rt△ADE≌Rt△DCF,得出线段之间的关系,进而将四边形的面积转化为矩形BCFE的面积与2个△CDF的面积,通过线段之间的转化,即可得出结论.
解答: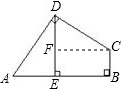 解:过点C作CF⊥DE交DE于F.
解:过点C作CF⊥DE交DE于F.
∵在△ADE与△DCF中,
,
∴△ADE≌△DCF(AAS),
∴DE=CF=BE,
又四边形ABCD的面积为8,即S矩形BCFE+2S△CDF=8,
即BE•EF+2×
CF•DF=8,
BE•DE=BE•BE=8,解得DE=2
.
故选:A.
 解:过点C作CF⊥DE交DE于F.
解:过点C作CF⊥DE交DE于F.∵在△ADE与△DCF中,
|
∴△ADE≌△DCF(AAS),
∴DE=CF=BE,
又四边形ABCD的面积为8,即S矩形BCFE+2S△CDF=8,
即BE•EF+2×
| 1 |
| 2 |
BE•DE=BE•BE=8,解得DE=2
| 2 |
故选:A.
点评:本题主要考查了全等三角形的判定及性质以及三角形、矩形面积的计算,能够熟练掌握.

练习册系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?