题目内容
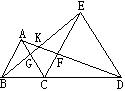
 如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的全等三角形对数有
如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的全等三角形对数有
- A.1对
- B.2对
- C.3对
- D.4对
C
分析:根据等边三角形的三边相等、三个角都是60°,以及全等三角形的判定方法(SSS、SAS、ASA、AAS),进行证明.
解答:△EBC≌△ACD,△GCE≌△FCD,△BCG≌△ACF.理由如下:
BC=AC,EC=CD,∠ACB=∠ECD,∠ACE是共同角?△EBC≌△ACD.
CD=EC,∠FCD=ECG,∠GEC=∠CDF?△GCE≌△FCD.
BC=AC,∠GBC=∠FAC,∠FCA=∠GCB?△BCG≌△ACF.
故选C.
点评:本题考查的是全等三角形的判定、等边三角形的性质以及旋转的性质的综合运用.
分析:根据等边三角形的三边相等、三个角都是60°,以及全等三角形的判定方法(SSS、SAS、ASA、AAS),进行证明.
解答:△EBC≌△ACD,△GCE≌△FCD,△BCG≌△ACF.理由如下:
BC=AC,EC=CD,∠ACB=∠ECD,∠ACE是共同角?△EBC≌△ACD.
CD=EC,∠FCD=ECG,∠GEC=∠CDF?△GCE≌△FCD.
BC=AC,∠GBC=∠FAC,∠FCA=∠GCB?△BCG≌△ACF.
故选C.
点评:本题考查的是全等三角形的判定、等边三角形的性质以及旋转的性质的综合运用.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 3、如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的全等三角形对数有( )
3、如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的全等三角形对数有( )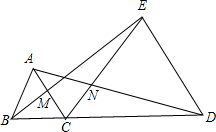 如图,C是线段BD上一点,分别以BC、CD为边长的BD同侧作等边三角形BCA和等边三角形CDE,连接BE、AD,分别交AC于M,交CE于N,若CM=x,则CN=
如图,C是线段BD上一点,分别以BC、CD为边长的BD同侧作等边三角形BCA和等边三角形CDE,连接BE、AD,分别交AC于M,交CE于N,若CM=x,则CN= 如图,C是线段BD上一点,分别以BC、CD为边作等边三角形ABC和CDE,连接AD、BE.求证:AD=BE.
如图,C是线段BD上一点,分别以BC、CD为边作等边三角形ABC和CDE,连接AD、BE.求证:AD=BE.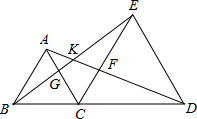 如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于点F,BE交AC于点G,则图中可通过旋转而相互得到的三角形是:
如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于点F,BE交AC于点G,则图中可通过旋转而相互得到的三角形是: