题目内容
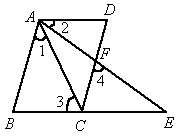
如图，已知△BCE、△ADC都是等边三角形．求证：AE=BD．分析：根据△BCE和△ADC是等边三角形，求证∠ACE=∠DCB，再利用SAS定理求证△ACE≌△DCB即可得出结论．
解答：证明：∵△BCE，△ADC是等边三角形，
∴AC=AD=DC，CE=CB=BE，∠ACD=∠BCE=60°，
∴∠ACD+∠DCE=∠BCE+∠DCE，
即∠ACE=∠DCB，
∴△ACE≌△DCB（SAS），
∴AE=BD．
∴AC=AD=DC，CE=CB=BE，∠ACD=∠BCE=60°，
∴∠ACD+∠DCE=∠BCE+∠DCE，
即∠ACE=∠DCB，
∴△ACE≌△DCB（SAS），
∴AE=BD．
点评：此题主要考查学生对等边三角形的性质和全等三角形的判定与性质的理解和掌握，此题的关键是求证∠ACE=∠DCB，比较简单，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
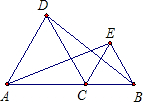
如图，已知△ABC的两条中线AD，BE相交于点F，得到8个图形：△ABD，△ACD，△BAE，△BCE，△FAB，△FAE，△FBD，四边形CEFD，现从中任取两个图形，求取得的这两个图形面积相等的概率．
ABCD的邻边BC、CD为边向外所作的等边三角形.求证：△AEF是等边三角形.
如图，已知△BCE、△ADC都是等边三角形．求证：AE=BD．