题目内容
在△ABC中，AD是BC边上的高，且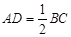
，E、F分别是AB、AC的中点，以EF为直径的圆与BC位置关系是（ ）
A. 相离 B. 相切； C. 相交； D. 相切或相交.
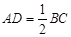，E、F分别是AB、AC的中点，以EF为直径的圆与BC位置关系是（ ）A. 相离 B. 相切； C. 相交； D. 相切或相交.
B
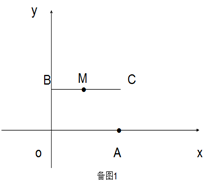
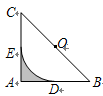
解：如图，
∵E，F分别是AB，AC的中点，
∴EF∥BC，EF=
BC，
∵AD是BC上的高，且AD= BC，
∴EF=AD，
∴OD=OA= AD= EF；
所以以EF为直径的圆的圆心到直线BC的距离等于OD
即以EF为直径的圆与BC的位置关系是相切．
故选B．
∵E，F分别是AB，AC的中点，
∴EF∥BC，EF=
BC， ∵AD是BC上的高，且AD=
BC，∴EF=AD，
∴OD=OA=
AD= EF；所以以EF为直径的圆的圆心到直线BC的距离等于OD
即以EF为直径的圆与BC的位置关系是相切．
故选B．
练习册系列答案
相关题目
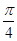
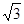米
