题目内容
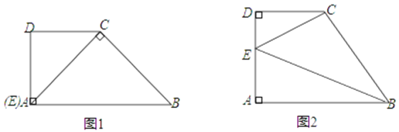
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() ,分别以
,分别以![]() 边所在直线为
边所在直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求点![]() 的坐标;
的坐标;
(2)已知![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点E作EG⊥x轴于G,且EG:OG=2.求直线
,过点E作EG⊥x轴于G,且EG:OG=2.求直线![]() 的解析式;
的解析式;
(3)点![]() 是(2)中直线
是(2)中直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上方的平面内是否存在一点
轴上方的平面内是否存在一点![]() ,使以
,使以![]() 为顶点的四边形为菱形?若存在,请求出
为顶点的四边形为菱形?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
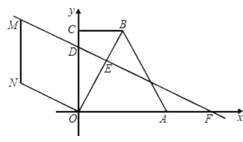
【答案】(1)![]() ;(2)
;(2)![]() ; (3)存在,
; (3)存在,![]() .
.
【解析】
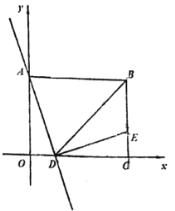
(1)如图过点B作BH⊥x轴,垂足为点H,则四边形OCBH为矩形,在Rt△ABH中,通过解直角三角形可求出BH的长度,进而可得出点B的坐标;
(2)作![]() 轴于点
轴于点![]() ,由平行可知
,由平行可知![]() ,得到
,得到![]() ,从而可求得EG的长度得到E点坐标,根据OD的长度可得出点D的坐标,再根据点D、E的坐标利用待定系数法即可求出直线DE的解析式;
,从而可求得EG的长度得到E点坐标,根据OD的长度可得出点D的坐标,再根据点D、E的坐标利用待定系数法即可求出直线DE的解析式;
(3)分OD为边及OD为对角线两种情况考虑:①当OD,DM为边时,作![]() 轴于点
轴于点![]() ,则
,则![]() 轴,通过相似和解直角三角形可求出点M的坐标,再根据菱形的性质即可求出点N的坐标(因为另一种情况点N在x轴下方,故可不考虑);②当OD,OM为边时,延长
轴,通过相似和解直角三角形可求出点M的坐标,再根据菱形的性质即可求出点N的坐标(因为另一种情况点N在x轴下方,故可不考虑);②当OD,OM为边时,延长![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() 轴,设点M的坐标为(a,-
轴,设点M的坐标为(a,-![]() a+5),由OM=OD=5,可得出关于x的一元二次方程,解之可得出点M的坐标,再利用菱形的性质可求出点N的坐标;③当OD为对角线时,连结
a+5),由OM=OD=5,可得出关于x的一元二次方程,解之可得出点M的坐标,再利用菱形的性质可求出点N的坐标;③当OD为对角线时,连结![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 与
与![]() 互相垂直平分,通过函数关系式可求出点M、N的横坐标,进而求出M、N的坐标.综上即可得出结论.
互相垂直平分,通过函数关系式可求出点M、N的横坐标,进而求出M、N的坐标.综上即可得出结论.
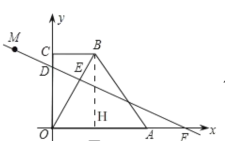
(1)如图,作![]() 于点
于点![]() ,则易得四边形
,则易得四边形![]() 为矩形,
为矩形,
![]()
![]()
在![]() 中
中![]() ,
,
∴![]() ,
,
∴点B的坐标为(3,6).
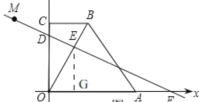
(2) 如图,作![]() 轴于点
轴于点![]() ,则
,则![]()
![]()
![]()
又![]()
![]()
![]()
![]()
又![]()
![]() ,D在y轴正半轴,
,D在y轴正半轴,
∴点![]() 的坐标为(0,5),设直线
的坐标为(0,5),设直线![]() 的解析式为:
的解析式为:![]()
则![]() 解得:
解得:![]()
![]() 直线
直线![]() 的解析式为,
的解析式为,![]()
(3)存在,
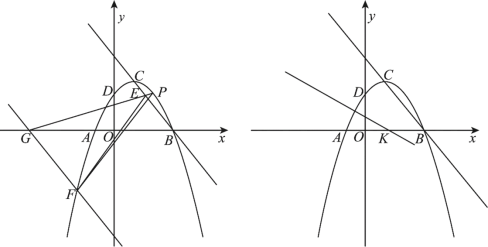
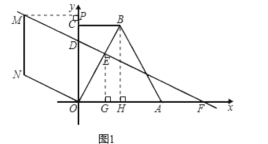
①如图1,当![]() ,四边形
,四边形![]() 为菱形.作
为菱形.作![]() 轴于点
轴于点![]() ,则
,则![]() 轴,
轴,
![]()
![]()
又![]() 时
时![]() 解得
解得![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
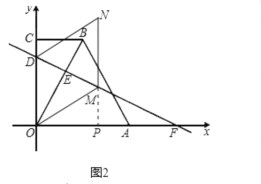
②如图2,当![]() 时,四边形
时,四边形![]() 为菱形,延长
为菱形,延长![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() 轴,
轴,
![]() 点
点![]() 在直线
在直线![]() 上
上
设![]()
在![]() 中,
中,![]()
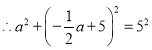 解得:
解得:![]()
![]()
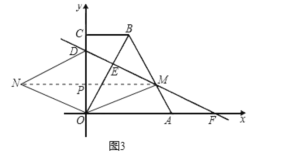
③如图3,当![]() 时,四边形
时,四边形![]() 为菱形,连结
为菱形,连结![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 与
与![]() 互相垂直平分,
互相垂直平分,
![]()
![]()
![]()
![]()
综上所述;![]() 轴上方的点
轴上方的点![]() 有三个,分别为
有三个,分别为
![]() .
.

 阅读快车系列答案
阅读快车系列答案