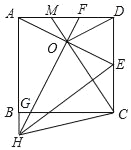
题目内容
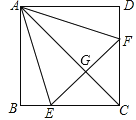
【题目】在![]() 中,
中,![]() ,分别以
,分别以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() .
.

(1)当![]() 时,正方形
时,正方形![]() 的周长
的周长![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
(2)连接![]() .试说明:三角形
.试说明:三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的一半.
面积的一半.
(3)已知![]() ,且点
,且点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是线段
是线段![]() 上的动点,当
上的动点,当![]() 点和
点和![]() 点在移动过程中,
点在移动过程中,![]() 的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
【答案】(1)4![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() 的周长最小值为
的周长最小值为![]()
【解析】
(1)根据正方形的周长公式即可得解;
(2)首先判定![]() ,然后即可判定
,然后即可判定![]() ,即可得解;
,即可得解;
(3)利用对称性,当A′、P、Q、F共线时![]() 的周长取得最小值,然后利用勾股定理即可得解.
的周长取得最小值,然后利用勾股定理即可得解.
(1)由题意,得正方形![]() 的周长为
的周长为![]() ;
;
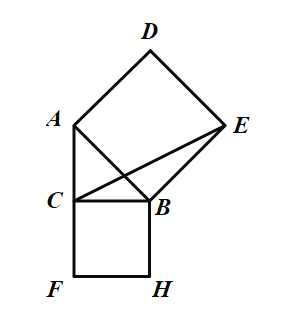
(2)连接![]() ,如图所示:
,如图所示:
∵∠CBH=∠ABE=90°
∴∠CBH+∠ABC=∠ABE+∠ABC
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() 的面积
的面积![]() 的面积
的面积![]() 正方形
正方形![]() 的面积
的面积
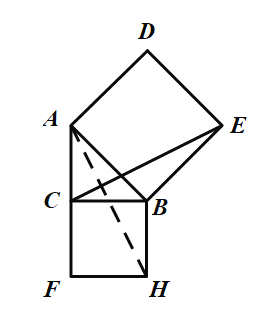
(3)作点![]() 关于
关于![]() 的对称点
的对称点![]() ,∴
,∴![]()
点![]() 关于
关于![]() 的对称点
的对称点![]() ,∴
,∴![]()
∵![]() 的周长为
的周长为![]() ,即为
,即为![]()
当A′、P、Q、F共线时![]() 的周长取得最小值,
的周长取得最小值,
∴![]() 的周长的最小值为
的周长的最小值为![]()
过![]() 作
作![]() 的延长线于
的延长线于![]() ,
,
∵![]()
∴∠CAB=45°,AB=AD=![]()
∵∠DAB=90°
∴∠MAA′=45°
∴![]() 为等腰直角三角形
为等腰直角三角形
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() 的周长最小值为
的周长最小值为![]() .
.


练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目