题目内容
当2＜x＜3时，
= ．
【答案】分析：首先根据已知条件判断出（2-x）、（x-3）的符号，然后再根据二次根式的性质进行化简．
解答：解：∵2＜x＜3，
∴2-x＜0，x-3＜0；
故原式=-（2-x）-（x-3）
=-2+x-x+3=1．
点评：二次根式
规律总结：当a≥0时，
=a；当a≤0时，
=-a．
能够正确的判断出a的符号，是解答此类化简题的关键．
解答：解：∵2＜x＜3，
∴2-x＜0，x-3＜0；
故原式=-（2-x）-（x-3）
=-2+x-x+3=1．
点评：二次根式
规律总结：当a≥0时，=a；当a≤0时，=-a．能够正确的判断出a的符号，是解答此类化简题的关键．
练习册系列答案
阅读快车系列答案
相关题目
的路程y（km）与时间x（h）的函数图象如图所示．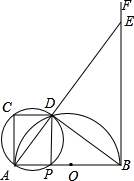
B重合），过A、P、C三点的圆与⊙O相交于除点A以外的另一点D，连接AD并延长交射线BF于点E，连接DB、DP、DC．
如图，在一个坡角为30°的斜坡上有一棵树，高AB，当太阳光与水平线成60°时，测得该树在斜坡上的树影BC的长为6m，则树高AB=
矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2．动点M、N分别从点D、B同时出发，沿线段DA、线段BA向点A的方向运动，当动点M运动到点A时，M、N两点同时停止运动．连接FM、FN．设点M、N的运动速度都是1个单位/秒，M、N运动的时间为x秒，问：当x为多少时，FM⊥FN？
抛物线上的一点C，使△OCA∽△OBC，且AC：BC=