题目内容
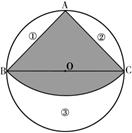
如图,有一块圆形铁皮,BC是⊙O的直径, |
| AB |
 |
| AC |
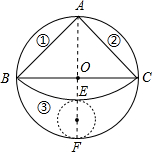 部分).
部分).(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留π).
(2)当⊙O的半径为R(R>0)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
分析:(1)先由圆的性质求得阴影部分扇形的半径,由直径所对的圆周角是90°可知圆心角的度数,可求得阴影部分的面积;
(2)先分别用R表示出阴影部分扇形的弧长,即所要围成的圆锥的底面周长为
Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-
)Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
(2)先分别用R表示出阴影部分扇形的弧长,即所要围成的圆锥的底面周长为
| ||
| 2 |
| 2 |
解答:解:∵BC是⊙O的直径,
=
∴∠BAC=90°,AB=AC,AF⊥BC
(1)当⊙O的半径为2时
AC=AB=2
∴S阴影=
=2π;
(2)当⊙O的半径为R(R>0)时
AC=AB=
R
阴影部分扇形的弧长为:
Rπ
EF=2R-
R
以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-
)Rπ
∵
Rπ>(2-
)Rπ
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
 |
| AB |
 |
| AC |
∴∠BAC=90°,AB=AC,AF⊥BC
(1)当⊙O的半径为2时
AC=AB=2
| 2 |
∴S阴影=
| 90π•8 |
| 360 |
(2)当⊙O的半径为R(R>0)时
AC=AB=
| 2 |
阴影部分扇形的弧长为:
| ||
| 2 |
EF=2R-
| 2 |
以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-
| 2 |
∵
| ||
| 2 |
| 2 |
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
点评:主要考查了扇形的面积计算以及圆锥的侧面展开图和底面圆之间的联系.本题的难点在于第2问,解决问题的关键是找到剩余材料中所能做的最大圆的圆周长,并与圆锥的底面周长比较大小来判断.

练习册系列答案
相关题目
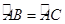 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分). );
);
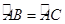 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).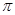 );
);
 =
= ,在此圆形铁皮中剪下一个扇形(阴影
,在此圆形铁皮中剪下一个扇形(阴影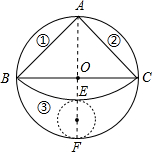 部分).
部分). =
= ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).