题目内容
 (1)如图(1),直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
(1)如图(1),直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.(2)如图(2),AB∥CD,BC∥DE,若∠B=50°18′,则∠D的度数是多少?
考点:平行线的判定与性质
专题:
分析:(1)根据平行线的判定得出AB∥CD,从而得出∠3=∠4,即可得出答案.
(2)首先根据平行线的性质可得∠B=∠C=50°18′,再根据BC∥DE可根据两直线平行,同旁内角互补可得答案.
(2)首先根据平行线的性质可得∠B=∠C=50°18′,再根据BC∥DE可根据两直线平行,同旁内角互补可得答案.
解答:解:(1)∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
∴∠4=∠3=75°(两直线平行,内错角相等).
(2):∵AB∥CD,
∴∠B=∠C=50°,
∵BC∥DE,
∴∠C+∠D=180°,
∴∠D=180°-50°18′=129°42′.
∴AB∥CD(同位角相等,两直线平行),
∴∠4=∠3=75°(两直线平行,内错角相等).
(2):∵AB∥CD,
∴∠B=∠C=50°,
∵BC∥DE,
∴∠C+∠D=180°,
∴∠D=180°-50°18′=129°42′.
点评:本题主要考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
 根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )
根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )| A、男生在13岁时身高增长速度最快 |
| B、女生在10岁以后身高增长速度放慢 |
| C、11岁时男女生身高增长速度基本相同 |
| D、9-10岁时女生身高比男生身高要高 |
二次函数y=(x-2)2-3的图象上最低点的坐标是( )
| A、(-2,-3) |
| B、(2,-3) |
| C、(-2,3) |
| D、(2,3) |
 如图是正方体的表面展开图,在正方形的A处填一个数,使它和相对面的数为相反数( )
如图是正方体的表面展开图,在正方形的A处填一个数,使它和相对面的数为相反数( )| A、2 | B、3 | C、-3 | D、-2 |
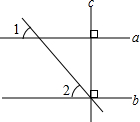 如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,
如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的余角等于( )
| A、60° | B、50° |
| C、40° | D、30° |
若三角形三个内角度数的比为2:3:4,则相应的外角比是( )
| A、2:3:4 |
| B、4:3:2 |
| C、7:6:5 |
| D、5:6:7 |
 如图,∠1+∠2=220°,b∥c,则∠3=( )
如图,∠1+∠2=220°,b∥c,则∠3=( )| A、110° | B、120° |
| C、70° | D、60° |
 一个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为
一个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为