题目内容
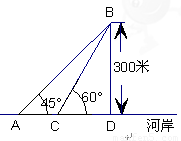
如图,某地海岸线可以近似地看作一条直线,两救生员在岸边A处巡查,发现在海中B处有人求救,救生员甲与乙都没有直接从A处游向B处,甲是沿岸边A处跑到离B最近的D处,然后游向B处;乙是沿岸边A处跑到点C处然后游向B处,若两救生员在岸边的行进速度都为6米∕秒,在海水中的行进速度都为2米∕秒,试分析救生员的选择是否正确?谁先到达点B处?( ,
, )
)
【答案】分析:因为速度已知,比较时间,需求路程,即求AB、AC、BC、BD的长以后再计算时间进行比较,解直角三角形ABD和BCD.
解答:解:∵BD=300,∠BAD=45°,
∴AD=300,
∴AB=300 ,
,
∴ =200(s)
=200(s)
在Rt△BCD中,CD= =100
=100 ,
,
BC= =200
=200 ,AC=AD-CD=300-100
,AC=AD-CD=300-100 ,
,
∴
∴t甲>t乙,
∴救生员的选择正确,救生员乙先到达.
点评:本题考查解直角三角形的应用,要注意运用三角关系及已知线段,本题综合性较强,有一定难度,同学们要细心求答.
解答:解:∵BD=300,∠BAD=45°,
∴AD=300,
∴AB=300
 ,
,∴
 =200(s)
=200(s)在Rt△BCD中,CD=
 =100
=100 ,
,
BC=
 =200
=200 ,AC=AD-CD=300-100
,AC=AD-CD=300-100 ,
,∴

∴t甲>t乙,
∴救生员的选择正确,救生员乙先到达.
点评:本题考查解直角三角形的应用,要注意运用三角关系及已知线段,本题综合性较强,有一定难度,同学们要细心求答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,某地海岸线可以近似地看作一条直线,两救生员在岸边A处巡查,发现在海中B处有人求救,救生员甲与乙都没有直接从A处游向B处,甲是沿岸边A处跑到离B最近的D处,然后游向B处;乙是沿岸边A处跑到点C处然后游向B处,若两救生员在岸边的行进速度都为6米∕秒,在海水中的行进速度都为2米∕秒,试分析救生员的选择是否正确?谁先到达点B处?(
如图,某地海岸线可以近似地看作一条直线,两救生员在岸边A处巡查,发现在海中B处有人求救,救生员甲与乙都没有直接从A处游向B处,甲是沿岸边A处跑到离B最近的D处,然后游向B处;乙是沿岸边A处跑到点C处然后游向B处,若两救生员在岸边的行进速度都为6米∕秒,在海水中的行进速度都为2米∕秒,试分析救生员的选择是否正确?谁先到达点B处?(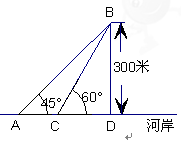
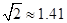 ,
,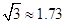 )
)
 ,
, )
)
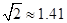 ,
,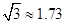 )
)