题目内容
设点O(0,0)、点A(2,0),分别以O、A为圆心,半径为2r、r作圆,两圆在第一象限 的交点为P.
的交点为P.
(1)当r=1时,求点P的坐标;
(2)当 时,能否找到一定点Q,使PQ为定值?若能找到,请求出Q点的坐标及定值;若不能找到,请说明理由.
时,能否找到一定点Q,使PQ为定值?若能找到,请求出Q点的坐标及定值;若不能找到,请说明理由.
解:(1)设P(x,y),
由勾股定理,得
解得 (舍去负值)
(舍去负值)
∴P( );
);
(2)设P(x,y),
由题意,得x2+y2=4[(x-2)2+y2]
化简,得x2+y2- x+
x+ =0
=0
即(x- )2+y2=
)2+y2=
∴定点为( ),定值为
),定值为 .
.
分析:(1)过P点作x轴的垂线,把△OPA分割成两个直角三角形,设P(x,y),在两个三角形中使用勾股定理,列方程组,解答本题;
(2)根据勾股定理,列方程求解.
点评:考查了运用勾股定理解二元二次方程组(二元二次方程)、圆与圆的位置关系与数量关系间的联系.此类题为中考热点,需重点掌握.
由勾股定理,得

解得
 (舍去负值)
(舍去负值)∴P(
 );
);(2)设P(x,y),
由题意,得x2+y2=4[(x-2)2+y2]
化简,得x2+y2-
 x+
x+ =0
=0即(x-
 )2+y2=
)2+y2=
∴定点为(
 ),定值为
),定值为 .
.分析:(1)过P点作x轴的垂线,把△OPA分割成两个直角三角形,设P(x,y),在两个三角形中使用勾股定理,列方程组,解答本题;
(2)根据勾股定理,列方程求解.
点评:考查了运用勾股定理解二元二次方程组(二元二次方程)、圆与圆的位置关系与数量关系间的联系.此类题为中考热点,需重点掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
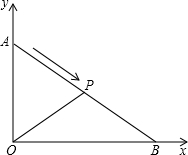 AB上的动点,点P以每秒2个单位的速度从点A向点B运动.设运动时间为t秒(0<t<5).
AB上的动点,点P以每秒2个单位的速度从点A向点B运动.设运动时间为t秒(0<t<5).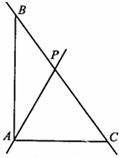 19、如图,在△ABC中,AB=12,AC=5,∠BAC=90°.若点P是BC的中点,则线段AP的长等于
19、如图,在△ABC中,AB=12,AC=5,∠BAC=90°.若点P是BC的中点,则线段AP的长等于 ,1).
,1).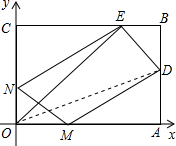
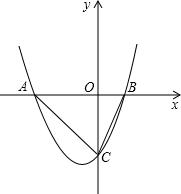 位置时,线段PQ的值最大,并求此时P点的坐标.
位置时,线段PQ的值最大,并求此时P点的坐标.