��Ŀ����
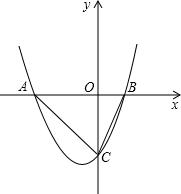
��ͼ����֪������y=| 1 | 2 |
��1����������ߵĽ���ʽ��
��2�����E���߶�AB�ϵĶ��㣬��EF��AC��BC��F������CE������CEF������ǡ�BEF�����2��ʱ����E������ꣻ
��3����PΪ��������A��C������һ�����㣬��P��y���ƽ���ߣ���AC��Q����P���˶���ʲô
 λ��ʱ���߶�PQ��ֵ������ʱP������꣮
λ��ʱ���߶�PQ��ֵ������ʱP������꣮
��������1����A��C��������������ߵĽ���ʽ�У������������ϵ����ֵ��
��2�����������ߵĽ���ʽ�ɵó�C������꣬��֤�á�ABC��ֱ�������Σ���EF��BC����CEF�͡�BEFͬ�ߣ�������ȵ��ڵױ߱ȣ��ɴ˿ɵó�CF=2BF����֤�á�BEF�ס�BAC���������������ε����ʣ��������BE��AB�ı�����ϵ���ɴ˿����E�����ꣻ
��3��PQ�ij�ʵ����ֱ��AC�������ߵĺ���ֵ�IJ����P�������Ϊm����m��ʾ��P��Q�������꣬Ȼ��ɵó�PQ�ij���m�ĺ�����ϵʽ���������ú��������ʼ������PQ���ʱ��m��ֵ��Ҳ���������ʱP������꣮
��2�����������ߵĽ���ʽ�ɵó�C������꣬��֤�á�ABC��ֱ�������Σ���EF��BC����CEF�͡�BEFͬ�ߣ�������ȵ��ڵױ߱ȣ��ɴ˿ɵó�CF=2BF����֤�á�BEF�ס�BAC���������������ε����ʣ��������BE��AB�ı�����ϵ���ɴ˿����E�����ꣻ
��3��PQ�ij�ʵ����ֱ��AC�������ߵĺ���ֵ�IJ����P�������Ϊm����m��ʾ��P��Q�������꣬Ȼ��ɵó�PQ�ij���m�ĺ�����ϵʽ���������ú��������ʼ������PQ���ʱ��m��ֵ��Ҳ���������ʱP������꣮
��� �⣺��1����A��C������������ʽ�ã�
�⣺��1����A��C������������ʽ�ã�
��
��ã�
��
��y=
x2+
x-2��
��2���ɣ�1��֪��C��0��-2����
��AC2=AO2+OC2=20��BC2=BO2+OC2=5��
��AB2=25=AC2+BC2��
���ACB��ֱ�������Σ��ҡ�ACB=90�㣻
��EF��AC��
��EF��BC��
��S��CEF=2S��BEF��
��CF=2BF��BC=3BF��
��EF��AC��
��
=
=
��
��AB=5��
��BE=
��
OE=BE-OB=
����E��-
��0����
��3����P��������m��
m2+
m-2����
 ��֪A��-4��0����C��0��-2����
��֪A��-4��0����C��0��-2����
��ֱ��AC�Ľ���ʽΪ��
y=kx-2��
����-4k-2=0��k=-
��
��ֱ��AC�Ľ���ʽΪy=-
x-2��
��Q��������m��-
m-2����
��PQ=-
m-2-��
m2+
m-2��=-
m2-2m��
�൱m=-2����P��-2��-3��ʱ��PQ��������ֵΪ2��
�ʵ�P�˶���OA��ֱƽ������ʱ��PQ��ֵ���ʱP��-2��-3����
 �⣺��1����A��C������������ʽ�ã�
�⣺��1����A��C������������ʽ�ã�
|
��ã�
|
��y=
| 1 |
| 2 |
| 3 |
| 2 |
��2���ɣ�1��֪��C��0��-2����
��AC2=AO2+OC2=20��BC2=BO2+OC2=5��
��AB2=25=AC2+BC2��
���ACB��ֱ�������Σ��ҡ�ACB=90�㣻
��EF��AC��
��EF��BC��
��S��CEF=2S��BEF��
��CF=2BF��BC=3BF��
��EF��AC��
��
| BE |
| AB |
| BF |
| BC |
| 1 |
| 3 |
��AB=5��
��BE=
| 5 |
| 3 |
OE=BE-OB=
| 2 |
| 3 |
| 2 |
| 3 |
��3����P��������m��
| 1 |
| 2 |
| 3 |
| 2 |
 ��֪A��-4��0����C��0��-2����
��֪A��-4��0����C��0��-2������ֱ��AC�Ľ���ʽΪ��
y=kx-2��
����-4k-2=0��k=-
| 1 |
| 2 |
��ֱ��AC�Ľ���ʽΪy=-
| 1 |
| 2 |
��Q��������m��-
| 1 |
| 2 |
��PQ=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
�൱m=-2����P��-2��-3��ʱ��PQ��������ֵΪ2��
�ʵ�P�˶���OA��ֱƽ������ʱ��PQ��ֵ���ʱP��-2��-3����
���������⿼���˶��κ�������ʽ��ȷ����ֱ�������ε��ж������ʡ�����������������������ε��ж������ʡ����κ�����Ӧ�õ�֪ʶ���ۺ���ǿ���ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
 C��0��3����
C��0��3���� ��C��0��-3�����㣬��x�ύ����һ��B��
��C��0��-3�����㣬��x�ύ����һ��B�� ��2013•��������ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=-1��
��2013•��������ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=-1�� ��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���������߾���A��-1��0����C��0��-3�����㣬��x�ύ����һ��B��
��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���������߾���A��-1��0����C��0��-3�����㣬��x�ύ����һ��B�� ��ͼ����֪������y=ax2+bx+c�Ķ����ǣ�-1��-4��������x�ύ��A��B��1��0�����㣬��y���ڵ�C��
��ͼ����֪������y=ax2+bx+c�Ķ����ǣ�-1��-4��������x�ύ��A��B��1��0�����㣬��y���ڵ�C��