Question

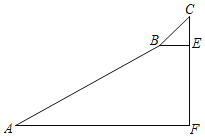
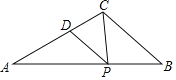
【题目】如图，在△ABC中，AB＝6，AC＝4，∠A＝30°，线段AB上有一个动点P，过点P作PD∥BC，交AC于D，连接PC，则△PCD的最大面积是_____．

Answer 1

【答案】

【解析】

过点C作CE⊥AB于E，过点P作PF⊥AC于F，先求出S△ACB＝×AB×CE＝6，通过证明△ADP∽△ACB，可得＝（）2，可求PF＝AD，由三角形面积公式可得S△PCD＝﹣（AD﹣2）2+，由二次函数的性质可求解．

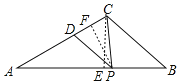
解：如图，过点C作CE⊥AB于E，过点P作PF⊥AC于F，

∵AC＝4，∠A＝30°，

∴CE＝AC＝2，

∴S△ACB＝×AB×CE＝6，

∵PD∥BC，

∴△ADP∽△ACB，

∴＝（）2，

∴S△ADP＝6×，

∴×AD×PF＝6×，

∴PF＝AD，

∵S△PCD＝×CD×PF＝×（4﹣AD）×AD＝﹣（AD﹣2）2+，

∴当AD＝2时，△PCD的最大面积＝，

故答案为：．