题目内容
如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部 分的图形仍然构成一个轴对称图形的概率是( )
分的图形仍然构成一个轴对称图形的概率是( )

A. 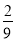 B.
B. 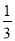 C.
C. 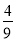 D.
D. 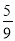
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
题目内容
如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部 分的图形仍然构成一个轴对称图形的概率是( )
分的图形仍然构成一个轴对称图形的概率是( )

A. 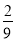 B.
B. 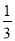 C.
C. 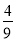 D.
D. 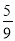
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案