题目内容
 如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:AE∥BC.
如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:AE∥BC.考点:相似三角形的判定与性质,等腰三角形的性质
专题:证明题
分析:利用相似可得到
=
,∠ACB=∠DCE,证明△BCD∽△ACE,可得到∠CAE=∠ACB则可证明AE∥BC.
| BC |
| CD |
| AC |
| CE |
解答:证明:
∵△ABC∽△EDC,
∴
=
,∠ACB=∠DCE,
∴∠BCD=∠ACE,
∴△BCD∽△ACE
∴∠CAE=∠B,
∴∠CAE=∠ACB,
∴AE∥BC.
∵△ABC∽△EDC,
∴
| BC |
| CD |
| AC |
| CE |
∴∠BCD=∠ACE,
∴△BCD∽△ACE
∴∠CAE=∠B,
∴∠CAE=∠ACB,
∴AE∥BC.
点评:本题主要考查相似三角形的性质和判定,掌握相似三角形的对应边成比例、对应角相等是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 要测一条河的宽度CD,先在河岸的一边引一条基线AB,再在A,B两点分别观测一点C.现测得∠CAB=α,∠CBA=β,AB=a米,求河宽CD.
要测一条河的宽度CD,先在河岸的一边引一条基线AB,再在A,B两点分别观测一点C.现测得∠CAB=α,∠CBA=β,AB=a米,求河宽CD.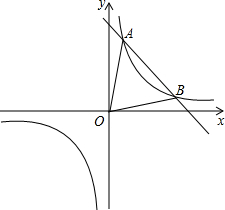 如图,一次函数y1=-x+5与反比例函数y2=
如图,一次函数y1=-x+5与反比例函数y2= 如图,已知DE是△ABC的中位线,点F是DE的中点,BF的延长线交AC于点G,求AG:GE的值.
如图,已知DE是△ABC的中位线,点F是DE的中点,BF的延长线交AC于点G,求AG:GE的值.