题目内容
如图，已知四边形OABC是菱形，CD⊥x轴，垂足为D，函数
的图象经过点C，且与AB交于点E．若OD=2，则△OCE的面积为
- A.2
- B.4
- C.2
- D.4
C
分析：连接AC，已知OD=2，CD⊥x轴，根据OD×CD=xy=4求CD，根据勾股定理求OC，根据菱形的性质，S△OCE=S△OAC=OA×CD求解．
解答：
解：连接AC，
∵OD=2，CD⊥x轴，
∴OD×CD=xy=4，
解得CD=2，由勾股定理，得OC=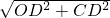
=2，
由菱形的性质，可知OA=OC，
∵△OCE与△OAC同底等高，
∴S△OCE=S△OAC=
×OA×CD=×2×2=2．
故选C．
点评：本题考查了反比例函数的综合运用．关键是求菱形的边长，讲所求三角形的面积进行转化．
分析：连接AC，已知OD=2，CD⊥x轴，根据OD×CD=xy=4求CD，根据勾股定理求OC，根据菱形的性质，S△OCE=S△OAC=OA×CD求解．
解答：
解：连接AC，∵OD=2，CD⊥x轴，
∴OD×CD=xy=4，
解得CD=2，由勾股定理，得OC=
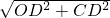=2，由菱形的性质，可知OA=OC，
∵△OCE与△OAC同底等高，
∴S△OCE=S△OAC=
×OA×CD=×2×2=2．故选C．
点评：本题考查了反比例函数的综合运用．关键是求菱形的边长，讲所求三角形的面积进行转化．
练习册系列答案
名校课堂系列答案
相关题目
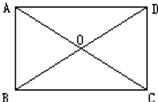7、如图，已知四边形ABCD，从下列任取3个条件组合，使四边形ABCD为矩形，把可能情况写出来（只填写序号即可，要求至少要写二个）
如图，已知四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD．
如图，已知四边形ABCD是平行四边形，下列结论中正确的是（ ）
如图，已知四边形ABCD，对角线AC，BD相交于点O．仅从下列六项条件中任意选取两项作为已知条件，就能够确定四边形ABCD是平行四边形的方法有（ ）种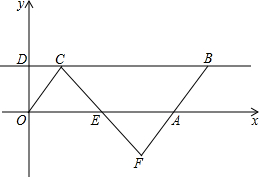
如图，已知四边形OAB是平行四边形（其中O为坐标原点），点A坐标为（4，0），BC所在直线l经过点D（0，1），E是OA边的中点，连接CE并延长，交线段BA的延长线于点F．