题目内容
已知⊙O过点D(3,4),点H与点D关于x轴对称,过H作⊙O的切线交x轴于点A.(1)求直线HA的函数解析式;
(2)求sin∠HAO的值;
(3)如图,设⊙O与x轴正半轴交点为P,点E、F是线段OP上的动点(与点P不重合),连接并延长DE、DF交⊙O于点B、C,直线BC交x轴于点G,若△DEF是以EF为底的等腰三角形,试探索sin∠CGO的大小怎样变化,请说明理由.

【答案】分析:(1)连OH,作HK⊥x轴于k,根据关于x轴对称的坐标特点得到H点坐标为(3,-4),再根据切线的性质由AH为⊙O的切线,得到OH⊥AH,利用等角的余角相等得到∠OAH=∠KHO,根据三角形相似的判定得RtAKH∽Rt△HKO,则AK:HK=HK:OK,即AK:4=4:3,求出AK= ,易得A点坐标为(
,易得A点坐标为( ,0),然后利用待定系数法求直线AH的解析式;
,0),然后利用待定系数法求直线AH的解析式;
(2)在Rt△OKH中,利用勾股定理计算出OH=5,然后在Rt△OAH中,利用正弦的定义即可得到sin∠HAO的值;
(3)过点D作DM⊥EF于M,并延长DM交⊙O于N,连接ON,交BC于T,根据垂径定理得到OM垂直平分DN,即D点与N点关于x轴对称,则N点坐标为(3,-4),ON=5;由DM⊥EF根据等腰三角形的性质可得DN平分∠BDC,即∠CDN=∠BDN,根据圆周角定理的推论得到弧BN=弧CN,然后利用垂径定理的推论可得OT⊥BC,利用等角的余角相等得到∠TGO=∠MNO,在Rt△OMN,OM=3,MN=4,利用正弦的定义即可得到sin∠MNO= =
= ,则sin∠CGO=
,则sin∠CGO= ,即sin∠CGO的大小不变.
,即sin∠CGO的大小不变.
解答:解:(1)如图,连OH,作HK⊥x轴于k,
∵点D(3,4),点H与点D关于x轴对称,
∴H点坐标为(3,-4),
∵AH为⊙O的切线,
∴OH⊥AH,
∴∠AOH+∠OAH=90°,∠KOH+∠KHO=90°,
∴∠OAH=∠KHO,
∴Rt△AKH∽Rt△HKO,
∴AK:HK=HK:OK,即AK:4=4:3,
∴AK= ,
,
∴OA=OK+AK=3+ =
= ,
,
∴A点坐标为( ,0),
,0),
设直线HA的函数解析式为y=kx+b,
把H(3,-4),A( ,0)代入得
,0)代入得 ,
,
解得 ,
,
∴直线HA的函数解析式为y= x-
x- ;
;
(2)在Rt△OKH中,OH= =5,
=5,
在Rt△OAH中,sin∠HAO= =
= =
= ;
;
(3)sin∠CGO的大小不变.理由如下:
过点D作DM⊥EF于M,并延长DM交⊙O于N,连接ON,交BC于T,如图,
则OM垂直平分DN,即D点与N点关于x轴对称,
则N点坐标为(3,-4),ON=5,
又∵△DEF为等腰三角形,DM⊥EF,
∴DN平分∠BDC,即∠CDN=∠BDN,
∴弧BN=弧CN,
∴OT⊥BC,
∴∠TGO+∠GOT=90°,
而∠MNO+∠MON=90°,
∴∠TGO=∠MNO,
在Rt△OMN,OM=3,MN=4,
∴sin∠MNO= =
= ,
,
∴sin∠CGO= .
.
即当E、F两点在OP上运动时(与点P不重合),sin∠CGO的值不变.
点评:本题考查了圆的综合题:圆的切线垂直于过切点的半径;垂直于弦的直径平分弦,并且平分弦所对的弧;平分弦所对的弧的直径垂直平分弦;在同圆或等圆中,相等的圆周角所对的弧相等;运用待定系数法求函数的解析式以及关于坐标轴对称的点的坐标特点;运用相似三角形的判定与性质和勾股定理进行几何计算.
 ,易得A点坐标为(
,易得A点坐标为( ,0),然后利用待定系数法求直线AH的解析式;
,0),然后利用待定系数法求直线AH的解析式;(2)在Rt△OKH中,利用勾股定理计算出OH=5,然后在Rt△OAH中,利用正弦的定义即可得到sin∠HAO的值;
(3)过点D作DM⊥EF于M,并延长DM交⊙O于N,连接ON,交BC于T,根据垂径定理得到OM垂直平分DN,即D点与N点关于x轴对称,则N点坐标为(3,-4),ON=5;由DM⊥EF根据等腰三角形的性质可得DN平分∠BDC,即∠CDN=∠BDN,根据圆周角定理的推论得到弧BN=弧CN,然后利用垂径定理的推论可得OT⊥BC,利用等角的余角相等得到∠TGO=∠MNO,在Rt△OMN,OM=3,MN=4,利用正弦的定义即可得到sin∠MNO=
 =
= ,则sin∠CGO=
,则sin∠CGO= ,即sin∠CGO的大小不变.
,即sin∠CGO的大小不变.解答:解:(1)如图,连OH,作HK⊥x轴于k,

∵点D(3,4),点H与点D关于x轴对称,
∴H点坐标为(3,-4),
∵AH为⊙O的切线,
∴OH⊥AH,
∴∠AOH+∠OAH=90°,∠KOH+∠KHO=90°,
∴∠OAH=∠KHO,
∴Rt△AKH∽Rt△HKO,
∴AK:HK=HK:OK,即AK:4=4:3,
∴AK=
 ,
,∴OA=OK+AK=3+
 =
= ,
,∴A点坐标为(
 ,0),
,0),设直线HA的函数解析式为y=kx+b,
把H(3,-4),A(
 ,0)代入得
,0)代入得 ,
,解得
 ,
,∴直线HA的函数解析式为y=
 x-
x- ;
;(2)在Rt△OKH中,OH=
 =5,
=5,在Rt△OAH中,sin∠HAO=
 =
= =
= ;
;(3)sin∠CGO的大小不变.理由如下:
过点D作DM⊥EF于M,并延长DM交⊙O于N,连接ON,交BC于T,如图,
则OM垂直平分DN,即D点与N点关于x轴对称,
则N点坐标为(3,-4),ON=5,
又∵△DEF为等腰三角形,DM⊥EF,
∴DN平分∠BDC,即∠CDN=∠BDN,
∴弧BN=弧CN,
∴OT⊥BC,
∴∠TGO+∠GOT=90°,
而∠MNO+∠MON=90°,
∴∠TGO=∠MNO,
在Rt△OMN,OM=3,MN=4,
∴sin∠MNO=
 =
= ,
,∴sin∠CGO=
 .
.即当E、F两点在OP上运动时(与点P不重合),sin∠CGO的值不变.
点评:本题考查了圆的综合题:圆的切线垂直于过切点的半径;垂直于弦的直径平分弦,并且平分弦所对的弧;平分弦所对的弧的直径垂直平分弦;在同圆或等圆中,相等的圆周角所对的弧相等;运用待定系数法求函数的解析式以及关于坐标轴对称的点的坐标特点;运用相似三角形的判定与性质和勾股定理进行几何计算.

练习册系列答案
相关题目
 如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC.已知圆过点C且与AC相交于F,与AB相切于AB的中点G.求证:AD⊥BF.
如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC.已知圆过点C且与AC相交于F,与AB相切于AB的中点G.求证:AD⊥BF.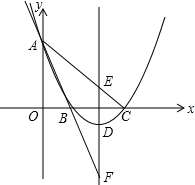 如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.