题目内容
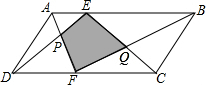如图，E、F分别是?ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q，若S△APD=12cm2，S△BQC=18cm2，则阴影部分的面积为考点：平行四边形的性质
专题：
分析：连接E、F两点，由三角形的面积公式我们可以推出S△EFC=S△BCQ，S△EFD=S△ADF，所以S△EFG=S△BCQ，S△EFP=S△ADP，因此可以推出阴影部分的面积就是S△APD+S△BQC．
解答：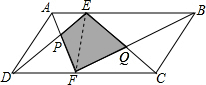
解：连接E、F两点，
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴△EFC的FC边上的高与△BCF的FC边上的高相等，
∴S△EFC=S△BCF，
∴S△EFQ=S△BCQ，
同理：S△EFD=S△ADF，
∴S△EFP=S△ADP，
∵S△APD=12cm2，S△BQC=18cm2，
∴S四边形EPFQ=30cm2，
故阴影部分的面积为30cm2．
故答案为：30cm2．
解：连接E、F两点，∵四边形ABCD是平行四边形，
∴AB∥CD，
∴△EFC的FC边上的高与△BCF的FC边上的高相等，
∴S△EFC=S△BCF，
∴S△EFQ=S△BCQ，
同理：S△EFD=S△ADF，
∴S△EFP=S△ADP，
∵S△APD=12cm2，S△BQC=18cm2，
∴S四边形EPFQ=30cm2，
故阴影部分的面积为30cm2．
故答案为：30cm2．
点评：本题主要考查平行四边形的性质，三角形的面积，解题的关键在于求出各三角形之间的面积关系．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
下面计算错误的是（ ）
| A、（-11）+（-17）=-28 | ||||||
B、
| ||||||
C、（-
| ||||||
| D、（-9）+9=0 |
若样本x1，x2，x3，…xn的平均数是10，方差是2，则对于样本（x1+1），（x2+1），（x3+1），…，（xn+1），下列结论中正确的是（ ）
| A、平均数为10，方差是2 |
| B、平均数是11，方差为3 |
| C、平均数为11，方差为2 |
| D、平均数为12，方差为4 |
用反正法证明命题“如图，如果AB∥CD，AB∥EF，那么CD∥EF”时，证明的第一个步骤是（ ）| A、假设AB不平行于CD |
| B、假设AB不平行于EF |
| C、假设CD∥EF |
| D、假设CD不平行于EF |
已知平面内两圆的半径分别为4和6，圆心距是4，则这两个圆的位置关系是（ ）
| A、相交 | B、内切 | C、外切 | D、外离 |
满足下列条件的△ABC不是直角三角形的是（ ）
A、BC=1，AC=2，AB=
| ||
| B、BC：AC：AB=3：4：5 | ||
| C、∠A+∠B=∠C | ||
| D、∠A：∠B：∠C=3：4：5 |
若A（-4，y1）、B（-2，y2）、C（3，y3）为抛物线y=x2+2x-3的图象上的三点，则y1，y2，y3的大小关系是（ ）
| A、y1＜y2＜y3 |
| B、y2＜y1＜y3 |
| C、y3＜y1＜y2 |
| D、y2＜y3＜y1 |