Question

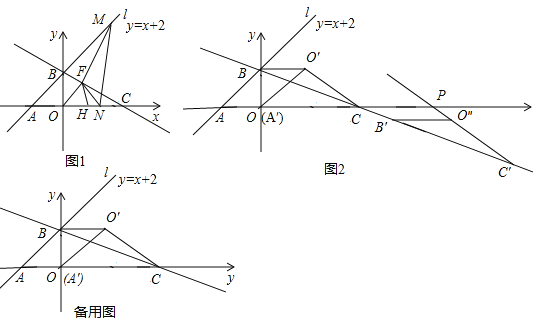
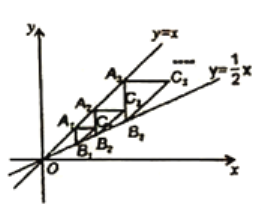
【题目】如图，点在直线上，过点作轴交直线于点，以点为直角顶点，为直角边在的右侧作等腰直角，再过点作轴，分别交直线和于，两点，以点为直角顶点，为直角边在的右侧作等腰直角按此规律进行下去，则等腰直角的面积为_______，等腰直角的面积为______．

Answer 1

【答案】，

【解析】

先根据点A1的坐标及A1B1∥y轴求出B1的坐标，进而得到A1B1的长及△A1B1C1的面积，再根据A2的坐标及A2B2∥y轴求出B2的坐标，进而得到A2B2的长及△A2B2C2的面积，根据变换规律A3B3的长得到△A3B3C3的面积，再求出AnBn的长得到△AnBnCn的面积即可.

∵A1（2,2），A1B1∥y轴交直线于点B1，

∴B1（2,1），

∴A1B1=2-1=1，

∴△A1B1C1的面积=11=，

∵A1C1= A1B1=1，

∴A2(3，3),

∵A2B2∥y轴交直线于点B2，

∴B2(3， ),

∴A2B2=3-=，

∴△A2B2C2的面积==，

∵A2C2= A2B2=，

∴A3(，)，

∵A3B3∥y轴交直线于点B3，

∴B3（， ），

∴A3B3=-=，

∴△A3B3C3的面积==，

∵△A1B1C1的面积=，

△A2B2C2的面积==，

△A3B3C3的面积=，

以此类推，△AnBnCn的面积=，

故答案为：， .