题目内容
解下列方程组
.
|
考点:高次方程
专题:
分析:先把方程组的第一个方程变形,得出两个方程,组成两个方程组,求出每个方程组的解,即可得出答案.
解答:解:∵2x2-xy-3x=0,
∴x(2x-y-3)=0,
x=0,2x-y-3=0,
即原方程组可以化为:①
,②
,
解方程组①得:
,
解方程组②得:
,
即方程组的解为:
,
.
∴x(2x-y-3)=0,
x=0,2x-y-3=0,
即原方程组可以化为:①
|
|
解方程组①得:
|
解方程组②得:
|
即方程组的解为:
|
|
点评:本题考查了解高次方程组的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
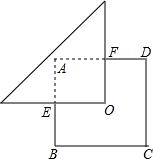 如图,O是边长为a的正方形ABCD的中心,将一块腰长足够长的等腰直角三角形纸板的直角顶点放在O处,并将纸板绕O点旋转.问正方形被纸板覆盖部分的面积是否发生变化.请说明理由.
如图,O是边长为a的正方形ABCD的中心,将一块腰长足够长的等腰直角三角形纸板的直角顶点放在O处,并将纸板绕O点旋转.问正方形被纸板覆盖部分的面积是否发生变化.请说明理由.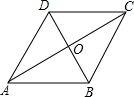 已知,如图在菱形ABCD中,对角线AC与BD相交于O,求证:AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
已知,如图在菱形ABCD中,对角线AC与BD相交于O,求证:AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.