题目内容
8.邮轮甲8:00从A港出发向西航行,10:00折向北航行,平均航速均为每小时20千米.邮轮乙在12:00正好在邮轮甲的正东方向和A港的东北方向上,求此时两船的距离.分析 作AE⊥CD于E,根据矩形的性质和等腰直角三角形的性质求出答案.
解答 解: 作AE⊥CD于E,
作AE⊥CD于E,
由题意得,AB=20×2=40千米,
BC=20×2=40千米,
则AE=BC=40千米,
∵AE⊥CD,∠D=∠EAD=45°,
∴DE=40千米,
∴CD=CE+DE=80千米,
答:此时两船的距离是80千米.
点评 本题考查的是解直角三角形的应用,根据题意正确画出图形、正确标注方向角是解题的关键.

练习册系列答案
相关题目
16.若四边形两条对角线相等,则顺次连接其各边中点得到的四边形是( )
| A. | 菱形 | B. | 矩形 | C. | 梯形 | D. | 正方形 |
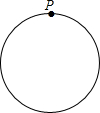 有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米
有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米
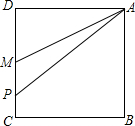 如图,在正方形ABCD的边CD上取一点P,使AP=PC+CB,M是DC的中点.求证:∠MAD=$\frac{1}{2}$∠BAP.
如图,在正方形ABCD的边CD上取一点P,使AP=PC+CB,M是DC的中点.求证:∠MAD=$\frac{1}{2}$∠BAP.